пʼятниця, 2 січня 2015 р.

Властивості бісектриси трикутника

Властивості бісектриси трикутника



Бісектри́са (лат. bis — двічі і лат. secare — розсікати, розтинати) — термін, що вживається вгеометрії для позначення кількох споріднених понять[1]:
  • Бісектриса кута — промінь, що проходить через вершину кута і ділить його навпіл. Кожна точка бісектриси однаково віддалена від сторін кута.
  • Бісектриса трикутника — відрізок бісектриси одного з кутів цього трикутника від вершини кута до перетину з протилежною стороною.

Властивості


Побудова бісектриси
  • Теорема про бісектрису: Бісектриса внутрішнього кута трикутника ділить протилежну сторону у відношенні, рівному відношенню двох прилеглих сторін
  • Бісектриси внутрішніх кутів трикутника перетинаються в одній точці — інцентрі — центрівписаного в цей трикутник кола.
  • Бісектриси одного внутрішнього та двох зовнішніх кутів трикутника перетинаються в одній точці. Ця точка — центр одного з трьох зовнівписаних кіл цього трикутника.
  • Основи бісектрис двох внутрішніх та одного зовнішнього кутів трикутника лежать на одній прямій, якщо бісектриса зовнішнього кута не є паралельною протилежній стороні трикутника.
  • Якщо бісектриси зовнішніх кутів трикутника не паралельні протилежним сторонам, то їх основи лежать на одній прямій.
  • Якщо в трикутнику дві бісектриси рівні, то трикутник — рівнобедрений (теорема Штейнера — Лемуса).
  • Побудова трикутника за трьома заданим бісектрисами за допомогою циркуля та лінійки неможлива,[2] причому навіть за наявностітрисектора.[3]
  • В рівносторонньому трикутнику бісектриса кута, протилежного до основи трикутника, є медіаною та висотою.
  • Відстані від сторін кута до будь-якої точки бісектриси однакові.
  • Кожна бісектриса трикутника ділиться точкою перетину бісектрис у відношенні суми довжин прилеглих сторін до довжини протилежної, рахуючи від вершини.

Формули за участю довжини бісектриси


Бісектриса трикутника. Виконується співвідношення BD: DC = AB: AC
l_c = {\sqrt{ab(a+b+c)(a+b-c)}\over{a+b}}
l_c = \sqrt{ab-a_lb_l}
l_c = \frac {2ab\cos\frac{\gamma}{2}}{a+b}
l_c = \frac {h_c}{\cos \frac {\alpha-\beta}{2}}
Де:
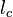  • l_c — бісектриса, проведена до сторони с
  • a, b, c — сторони трикутника проти вершин A, B,C відповідно
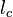  • a_l, b_l — довжини відрізків, на які бісектриса l_c ділить сторону с
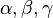  • \alpha, \beta, \gamma — внутрішні кути трикутника, що лежать навпроти сторін а, b,c відповідно
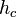  • h_c — висота трикутника, опущена на сторону c.



БІСЕКТРИСА ТРИКУТНИКА

Бісектриса трикутника – це відрізок бісектриси кута трикутника, що сполучає вершину трикутника з точкою на протилежній стороні. Трикутник має три бісектриси, які прийнято позначати lа, lb, lс. Запам’ятаємо, що з вершини А виходить бісектриса lа,, з вершини В виходить бісектриса lb з вершини С виходить бісектриса lс. Отже, бісектриса трикутника ділить величини кутів трикутника навпіл.
Зауваження. Необов’язково бісектриса ділить протилежну сторону навпіл.  Але у рівнобедреному та у рівносторонньому трикутнику, якщо бісектриса проведена до основи обов’язково поділить навпіл крім кута  і  сторону, яку перетинає. 

ВЛАСТИВОСТІ БІСЕКТРИС ТРИКУТНИКА.

1. Із трьох бісектрис трикутника, найбільша бісектриса виходить із найменшого кута, а найменша бісектриса виходить із найбільшого кута трикутника. Із рівних кутів виходять рівні бісектриси трикутника. Отже, якщо a ≤ b ≤ c тоді lс ≤  lb ≤ lа,

2. Із трьох бісектрис трикутника, найбільша бісектриса ділить найменшу сторону на дві необов’язково рівні частини, а найменша бісектриса ділить найбільшу сторону на дві необов’язково рівні частини.
3. Будь-яка бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні прилеглим сторонам трикутника. Тобто, якщо бісектриса проведена з вершини В та перетинає протилежну сторону в точці D, то маємо АL1: L1C = AB:BC.
 4. Усі три бісектриси трикутника перетинаються в одній точці, рівновіддаленій  від трьох сторін трикутника, тобто,  точка перетину бісектрис – це центр кола, що вписаний в трикутник. Точку перетину бісектрис називають  інцентром  трикутника.
5. Кут між бісектрисами, або центральний кут вписаного в трикутник кола, сторони якого проходять через вершини трикутника, рівний сумі прямого кута та половині кута через який не проходять сторони центрального кута. ÐВІС = 90о + 0,5α, ÐАІС = 90о + 0,5β,  ÐВІА = 90о + 0,5γ
 6. У довільному трикутнику бісектриса проходить між висотою та медіаною трикутника.  За трьома сторонами трикутника можна знайти довжини бісектрис трикутника

7. Бісектриса  зовнішнього кута трикутника перетинає продовження протилежної сторони в точці, відстані від якої до кінців цієї сторони пропорційні прилеглим сторонам.
8. Продовження бісектрис внутрішніх кутів трикутника проходить через центри зовні вписаних кіл(коло, яке дотикається  до однієї сторони та до продовження двох інших сторін трикутника), які являються точками перетину бісектрис зовнішніх кутів цього трикутника.
9. Кут між бісектрисами внутрішнього і зовнішнього кута трикутника прямий.
10. Бісектриси трикутника точкою перетину  діляться у відношенні,  сумі сторін до третьої, на яку проведено бісектрису: АI:IL1 =  (AB+AC):BC;   BI:IL2 = (AB+BC):AC;       CI:IL3 = (CB+CA):AB.
11.  Якщо дві бісектриси рівні, то трикутник рівнобедрений.
12. Квадрат бісектриси трикутника дорівнює різниці добутку сторін, що утворюють відповідний кут і добутку відрізків, на які вона розділяє третю сторону:
 АL1 2 =  AB∙AC – BL1 ∙L1C;         BL2 2 =AB∙BC – AL2 ∙L2C;       CL3 2 = CB∙CA – AL3∙ L3B. 
13. Пряма, що проходить через інцентр трикутника поділяє площу і периметр в одному і тому самому відношенні.
14. Площі двох трикутників, на які розрізає бісектриса трикутника відносяться як сторони даного трикутника, що відповідають сторонам розрізаних трикутників: SACL1: SABL1 = AC:AB;   SAВL2: SСBL2 = AВ:СB;  SAСL3: SСBL3 = AС:СB; 

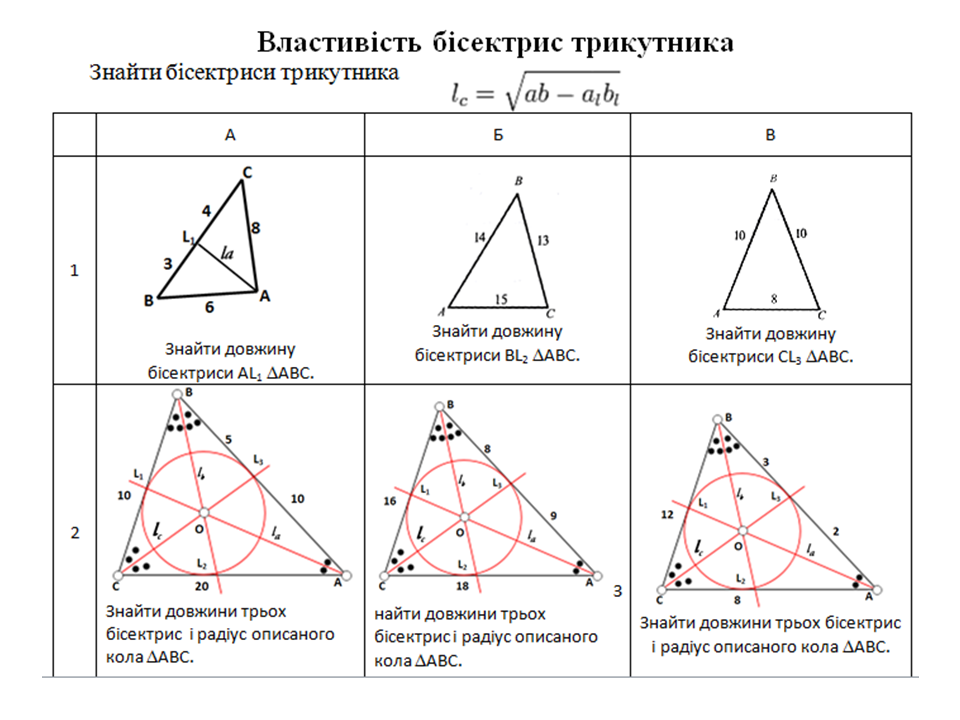
ЗАДАЧІ НА ВЛАСТИВОСТІ БІСЕКТРИС ТРИКУТНИКА.

1А.Кути DАВС відносяться, як α:β:γ =2:3:4. Розмістити  в порядку зростання: а) довжини сторін, б) довжини бісектрис. Чи можуть бісектриси перетинатися за межами DАВС? Який вид DАВС?
1Б. Сторони DАВС: а = 3 см,  b = 4 см  c = 5см. Розмістити  в порядку зростання: а) величини кутів, б) довжини бісектрис. Чи можуть бісектриси перетинатися у вершині DАВС? Який вид DАВС?
2А. Накресли прямокутний рівнобедрений DАВС. Провести в ньому три бісектриси. Яка бісектриса  рівна половині найбільшої сторони DАВС? Знайти кути між двома довільними бісектрисами DАВС?
2Б. Накресли прямокутний DАВС, ÐС=90о, ÐА=30о.   Провести в ньому медіану СМ, висоту СН, бісектрису CL із прямого кута. Знайти кут між бісектрисою CL і висотою СН  та кут між бісектрисою CL і медіаною СМ? Знайти кути між двома бісектрисами гострих кутів DАВС? Який вид DMCL?
3А. Бісектриса DАВС утворює з протилежною сто­роною кут 90°, а інша бісектриса з протилежною стороною утворює теж кут 90°. Який вид DАВС?
3Б. DАВС = DМАВ. АВ=ВС=АС. Чи обов’язково рівні відповідні бісектриси цих трикутників? Знайти кути між двома бісектрисами DАВС? Який вид DАВС?
4А. DАВС= DКМN, ÐК = 90°, ÐМ = 60°. Знайди всі кути DАВС, що утворилися в результаті перетину трьох бісектрис. Який вид DАВС?
4Б. Один з кутів DАВС дорівнює 20°, а один з двох інших в 4 рази більший другого. Яка найменша бісектриса DАВС? Який вид DАВС?
7. У рівнобедреного трикутника АВС знайди довжини бісектрис, якщо бічна СВ = 43 м, АВ = 10 м.
9. Кут між бісектрисою і стороною, що проведені з однієї вершини рівнобедреного трикутника, дорівнює 10°, а один з двох інших кутів трикутника дорівнює 70°. Знайди усі  невідомі кути в середині трикутника, що утворилися в результаті перетину бісектрис.
10. Знайди прямокутний трикут­ник, якщо у нього є дві рівні бісектриси.
11. Обчислити довжини  бісектрис трикутника, знаючи, сторони трикутника: 1) 2, 4, 4; 2) 4, 3, 5; 3) 2, 4; 5;  4) 2, 7, 3; б) 8, б, 5. Знайти довжини відрізків, на які ділиться кожна сторона трикутника бісектрисою.
12. Скільки рівних бісектрис у рівнобедреного трикутника. Накресліть будь-який трикутник та вкажіть центр вписаного в трикутник кола.. Перевірте цю властивість вписавши в нього коло.
13. Бісектриса, що проведена до основи рівнобедреного три­кутника нахилена до його основи під кутом 78°. Знайти кути цього трикутника. Скільки розв’язків має задача?
14. У трикутника три рівні бісектриси. Який вид цього трикутника?
15. У трикутника бісектриса ділить  сторону навпіл . Чи може цей трикутник бути прямокутним?( Тупокутним? Гострокутним?)
16. Периметр рівнобедреного трикутника 18 см, біч­на сторона на 3 см довша від основи.   Знайти   бісектриси  цього трикутника.

Завдання для самостійного закріплення умінь 
та навичок досліджувати та аналізувати

1.Скільки рівних трикутників можна утворити, провівши бісектриси рівностороннього трикутника?
2.На скільки тупокутних трикутників може поділити прямокутний  трикутник дві  його бісектриси?
3.Чи завжди будь-які три відрізки можуть бути бісектрисами трикутника?
4.Чи відповідні бісектриси нерівних трикутників можуть виявитися  рівними?
5.Відновити на довільному тупокутному трикутнику бісектриси стандартного трикутника. Виміряти їх та знайти суму їх, порівняти з периметром трикутника.
 
6. Визначити довжини бісектрис трикутників, у яких величини сторін: а)46м, 46м, 19м. б)35м,35м,35м. в) 7м, 7м, 9м?
 7.Скільки рівних трикутників можна утворити бісектрисами рівностороннього трикутника?
 8.Чи існують трикутники, у яких до найменшої сторони проведена найменша за довжиною бісектриса?
9.Яка середня за величиною бісектриса в трикутнику АВС, якщо:
 1) а = 5 см; b = 6 cм, с = 7 см?   2) а = 8 см; b = 6 cм, с = 5 см?   3) а = 7см; b = 9 cм, с = 8 см?  4) а = 8 см; b = 8 cм, с = 9 см?  5) а = 5 см; b = 5 cм, с = 5 см?
Запишіть бісектриси в порядку спадання. Знайти довжини сторін, на які ділиться кожна сторона трикутника бісектрисою.
 10. Яка найбільша бісектриса в трикутнику АВС, якщо
1) 35о, 78о; 2) 45о ,    130о; 3) 74о, 59о?
4)   97о,   18о?
5)   45 о ,     67 о?
6)   72 о ,    78 о?
Запишіть бісектриси цих трикутників у порядку зростання, не шукаючи їх довжини.
Задачі для самостійних дослідів учнів.
1.Яким повинен бути вид прямокутного трикутника, щоб довжина його найменшої сторони була рівна довжині бісектриси, що проведена до найбільшої сторони?
2.А  яким повинен бути вид трикутника , щоб усі бісектриси трикутника були різні? Замалювати кожний можливий випадок.
Підсумок заняття. Фронтальне опитування

Які основні  властивості бісектрис трикутника ми вивчаємо напам’ять? Як їх формулюють? Які властивості співвідношень у сторін та бісектрис
Задачі  на властивість бісектрис трикутника

1. BD-бісектриса кута В трикутника АВС. Знайти:
1)відрізки AD і DC,якщо АВ=8см, ВС=14см, АС=11см;
2)сторону АВ, якщo AD : DC = 7:8, BC =24см;
3)сторону АС ,якщо АВ: ВС=2:3,CD-AD=3см;
4)сторони АВ,ВС і АС,якщо АВ +ВС=56см, AD=9см, DC=15см.

2.Точка D лежить на стороні АВ трикутника АВС.
Порівняти кути ACD і BCD,якщо АС=12см,ВС= 15 см,AD=6смBD=12см.

3.Бісектриса гострого кута гострого кута прямокутного трикутника ділить протилежний катет у відношенні 2:1.Знайти гострі кути трикутника.

4.Бісектриса прямого кута прямокутного трикутника ділить гіпотенузу на відрізки довжиною 15см і 20см.Знайти катети.

5.Бісектриса гострого кута прямокутного трикутника ділить катет у відношенні 5:3,а різниця цих відрізків дорівнює 6см.Знайти сторони трикутника.

6.Висота BD трикутника АВС дорівнює 24см і ділить сторону АС на відрізки
AD=7см i DC=10см. На які відрізки ділить сторону АС бісектриса кута В?

7.Периметр прямокутника дорівнює 42см ,а його діагональ ділиться бісектрисою прямого кута на відрізки,довжини яких відносяться як3:4.Знайти діагональ прямокутника.

8.Бісектриса кута прямокутника ділить його сторону  на відрізки довжиною 10см і 14см,починаючи від найближчої до цього кута вершини. На які відрізки ділить ця бісектриса діагональ прямокутника.

9.Діагональ рівнобічної трапеції ділить висоту,проведену з вершини тупого кута,на відрізки довжиною 15см і 12см,а бічна сторона трапеції дорівнює її меншій основі. Знайти сторони трапеції.


10.У трикутник АВС вписано ромб ADEF так,що кут А у них спільний, а вершина Е належить стороні ВС.З найти довжини відрізків ВЕ і ЕС,якщо АВ=21см, ВС=18см, АС=15см.
Запитання для повторення з теми «Трикутник»


1.      Яку фігуру називають трикутником?
2.      Що називають стороною трикутника?
3.      Скільки сторін у трикутника?
4.      Що таке кут в трикутнику?
5.      Що називають висотою трикутника?
6.      Що називають медіаною трикутника?
7.      Що називають бісектрисою трикутника?
8.      Який трикутник називають рівнобедреним?
9.      Які властивості має рівнобедрений трикутник?
10.  В якому трикутнику кути при основі рівні?
11.  Які трикутники називають рівними?
12.  Як формулюється перша ознака рівності трикутників?
13.  Як формулюється  друга ознака рівності трикутників?
14.  Як формулюється третя ознака рівності трикутників?
15.  Який трикутник називають прямокутним?
16.  Як формулюється перша ознака рівності прямокутних трикутників?
17.  Як формулюється друга ознака рівності прямокутних трикутників?
18.  Як формулюється третя ознака рівності прямокутних трикутників?
19.  Які трикутники називають подібними?
20.  Як формулюється перша ознака подібності трикутників?
21.  Як формулюється друга ознака подібності трикутників?
22.  Як формулюється третя ознака подібності трикутників?
23.  Як формулюється перша ознака подібності прямокутних трикутників?
24.  Як формулюється друга ознака подібності прямокутних трикутників?
25.  Як формулюється третя ознака подібності прямокутних трикутників?
26.  Яка  властивість точки перетину медіан трикутника?
27.  Яка властивість бісектриси внутрішнього кута трикутника?
28.  Яка властивість висоти, опущеної з вершини прямого кута на гіпотенузу?
29.  Яка залежність між катетом та його проекцією на гіпотенузу в прямокутному трикутнику?
30.  Як формулюється теорема Піфагора?
31.  Де знаходиться центр кола, вписаного в трикутник?
32.  Де знаходиться центр кола, описаного навколо трикутника?
33.  Які трикутники називають правильними?
34.  Яка властивість кутів правильного трикутника?
35.  Де знаходиться центр симетрії правильного трикутника?
36.  Як обчислюється висота правильного трикутника?
37.  Як обчислюється радіус кола, вписаного в правильного трикутник?
38.  Як обчислюється радіус кола, описаного навколо правильного трикутника?
39.  Як обчислюється радіус кола, вписаного в довільний трикутник?
40.  Як обчислюється радіус кола, описаного навколо довільного трикутника?
41.  Як визначають тригонометричні функцій в прямокутному трикутнику?
42.  Як формулюється теорема синусів?

43.  Як формулюється теорема косинусів?





Контрольна робота з теми «Подібність трикутників»
Варіант 1.

Початковий та середній рівень.

У завданнях 1-6 виберіть правильну відповідь.
1.(1 бал) Сторони DАВС а = 3 м, b = 4 м, c = 5 м. Знайдіть найменшу сторону подібного йому DА1В1С1, якщо найбільша сторона с1 = 2,5 м.
А) 6 м;    Б) 2 м;       В) 1,5 м;      Г) 2,5 м;       Д) інша відповідь.
2. (1 бал) Точки М та Р лежать відповідно на сторонах  АВ та СВ DАВС, причому РМççАС. Знайдіть сторону  ВС, якщо АС =12  м, МР = 4 м, ВР = 5 м.
А)15 м;    Б) 10 м;       В) 12 м;      Г) 18 м;       Д) інша відповідь.
3. (1 бал) Відрізки АВ та МР перетинаються в точці О, АО:ОВ = РО:ОМ = 2:3,  ВМ=15 м. Знайдіть довжину відрізка АС.
А)18 м;    Б) 22,5 м;       В) 10 м;      Г) 5 м;       Д) інша відповідь.
4. (1 бал) Сторони DАВС а=10 м, b =20 м, c = 15 м. Дві сторони іншого трикутника дорівнюють    5 м та 7,5 м. Яка має бути довжина третьої сторони, якщо ці трикутники є подібними?
А) 40 м;    Б) 4 м;       В) 30 м;      Г) 10 м;       Д) інша відповідь.
5. (1 бал)  СН – висота прямокутного DАВС(ÐС =90о).  АН = 8 м, НВ = 18 м. Знайдіть довжини СН, АС, СВ.
А) 7 м; 14 м; 15 м;     Б) 4 м; 12 м; 14 м;     В) 6  м;  1 0м; 12 м;     Г) 8 м;  9 м; 10 м;          Д) інша відповідь.
6. (1 бал) ВК – бісектриса DАВС, АС = 14 м, СВ = 6 м, СК= 4 м.  Знайдіть довжину АВ.
А) 15 м;    Б) 14 м;       В) 10 м;      Г) 12 м;       Д) інша відповідь.

Достатній та високий рівень.

У завданнях 7-12 виконайте малюнки подібних трикутників  і детально обґрунтуйте свою відповідь.
7. (1 бал)  Сторони DАВС а = 6 м, b = 9 м, c =12 м. Знайдіть периметр подібного йому трикутника, якщо сума найменшої і найбільшої сторін дорівнює 9 м.
8. (1 бал)  Діагоналі чотирикутника АВСD – перетинаються в точці О.  Відомо, що АО∙ОВ =СО∙ОD.  Доведіть, що у чотирикутника АВСD є дві паралельні сторони. Чи можна цей чотирикутник вважати:  а) трапецією; б) паралелограмом?
9. (1 бал)  Сторони DАВС а=13 м, b =14 м, c =15 м. Знайдіть  довжини трьох бісектрис DАВС.
10. (1 бал)  Сторони DАВС  а = 6 м, b = 8 м, c = 10 м. Знайдіть  відношення відрізків на трьох бісектрисах, які утворюються точкою перетину бісектрис D АВС.
11. (1 бал)   Сторони DАВС  а = 5 м, b = 12 м, c = 13 м. Знайдіть  радіус кола, вписаного в DАВС.
12. (1 бал)  Хорди кола АВ і СD перетинаються в точці О.  Відомо, що АО:ОВ = 6:1, СО:ОD = 2:3, АО - ОВ =20 м. Знайдіть відрізки, на які точка О розбиває хорди АВ і СD.



Контрольна робота з теми «Подібність трикутників»
Варіант 2.

Початковий та середній рівень.

У завданнях 1-6 виберіть правильну відповідь.
1.(1 бал) Сторони DАВС а = 8 м, b = 6 м, c = 10 м. Знайдіть найменшу сторону подібного йому DА1В1С1, якщо найбільша сторона с1 = 12 м.
А) 20 м;    Б) 5 м;       В) 16 м;      Г) 4 м;       Д) інша відповідь.
2. (1 бал) Точки М та Р лежать відповідно на сторонах  АВ та СВ DАВС, причому РМççАС. Знайдіть сторону  МР, якщо АС =16  м,  СВ = 8 м, ВР = 5 м.
А)12 м;    Б) 8 м;       В) 12 м;      Г) 18 м;       Д) інша відповідь.
3. (1 бал) Відрізки АВ та МР перетинаються в точці О, АО:ОВ = РО:ОМ = 3:5,  АС = 6 м. Знайдіть довжину відрізка ВР.
А)20 м;    Б) 12 м;       В) 8 м;      Г) 10 м;       Д) інша відповідь.
4. (1 бал) Сторони DАВС а =6 м, b = 9 м, c = 13 м. Дві сторони іншого трикутника дорівнюють    3 м та 4,5 м. Яка має бути довжина третьої сторони, якщо ці трикутники є подібними?
А) 26 м;    Б) 6,5 м;       В) 7,5 м;      Г) 5 м;       Д) інша відповідь.
5. (1 бал)  СН – висота прямокутного DАВС(ÐС =90о).  АН = 5 м, НВ = 20 м. Знайдіть довжини СН, АС, СВ.
А) 8 м; 14 м; 13 м;     Б) 10 м; 12 м; 14 м;     В) 10 м;  11 м; 12 м;     Г) 8 м;  9 м; 10 м;          Д) інша відповідь.
6. (1 бал) ВК – бісектриса DАВС, АС = 16 м, СВ = 9 м, СК= 6 м.  Знайдіть довжину АВ.
А) 15 м;    Б) 9 м;       В) 12 м;      Г) 24 м;       Д) інша відповідь.

Достатній та високий рівень.
У завданнях 7-12 виконайте малюнки подібних трикутників  і детально обґрунтуйте свою відповідь.
7. (1 бал)  Сторони DАВС а = 6 м, b = 9 м, c = 12 м. Знайдіть периметр подібного йому трикутника, якщо сума найменшої і найбільшої сторін дорівнює 6 м.
8. (1 бал)  Висоти  АН1 та СН2 різностороннього DАВС – перетинаються в точці О.    Доведіть, що DАВС і DН1ВН2 є подібними. Чи можна чотирикутник АН2Н1С вважати:  а) трапецією; б) рівнобічною трапецією?
9. (1 бал)  Сторони DАВС а =21 м, b =14 м, c =15 м. Знайдіть  довжини трьох бісектрис DАВС.
10. (1 бал)  Сторони DАВС  а = 9 м, b = 12 м, c =15 м. Знайдіть  відношення відрізків на трьох бісектрисах, які утворюються точкою перетину бісектрис D АВС.
11. (1 бал)   Сторони DАВС  а = 8 м, b = 15 м, c = 17 м. Знайдіть  радіус кола, вписаного в DАВС.
12. (1 бал)  Хорди кола АВ і СD перетинаються в точці О.  Відомо, що АО:ОВ = 3:4, СО:ОD = 3:1, СО - ОD = 16 м. Знайдіть відрізки, на які точка О розбиває хорди АВ і СD.




Контрольна робота з теми «Подібність трикутників»
Варіант 3.
Початковий та середній рівень.
У завданнях 1-6 виберіть правильну відповідь.
1.(1 бал) Сторони DАВС  а = 8 м, b = 15 м, c = 17 м. Знайдіть найменшу сторону подібного йому DА1В1С1, якщо найбільша сторона с1 = 51 м.
А) 16 м;    Б) 32 м;       В) 30 м;      Г) 24 м;       Д) інша відповідь.
2. (1 бал) Точки М та Р лежать відповідно на сторонах  АВ та СВ DАВС, причому РМççАС. Знайдіть сторону  МР, якщо АС =20  м,  СВ = 10 м, ВР = 8 м.
А)12 м;    Б) 8 м;       В) 12 м;      Г) 18 м;       Д) інша відповідь.
3. (1 бал) Відрізки АВ та МР перетинаються в точці О, АО:ОВ = РО:ОМ = 1:3,  АС = 16 м. Знайдіть довжину відрізка ВР.
А)20 м;    Б) 12 м;       В) 8 м;      Г) 10 м;       Д) інша відповідь.
4. (1 бал) Сторони DАВС а = 6 м, b = 9 м, c = 13 м. Дві сторони іншого трикутника дорівнюють    3 м та 4,5 м. Яка має бути довжина третьої сторони, якщо ці трикутники є подібними?
А) 26 м;    Б) 6,5 м;       В) 7,5 м;      Г) 5 м;       Д) інша відповідь.
5. (1 бал)  СН – висота прямокутного DАВС(ÐС =90о).  АН = 5 м, НВ = 20 м. Знайдіть довжини СН, АС, СВ.
А) 8 м; 14 м; 13 м;     Б) 10 м; 12 м; 14 м;     В) 10 м;  11 м; 12 м;     Г) 8 м;  9 м; 10 м;          Д) інша відповідь.
6. (1 бал) ВК – бісектриса DАВС, АС = 16 м, СВ = 9 м, СК= 6 м.  Знайдіть довжину АВ.
А) 15 м;    Б) 9 м;       В) 12 м;      Г) 24 м;       Д) інша відповідь.
Достатній та високий рівень.
У завданнях 7-12 виконайте малюнки подібних трикутників
 і детально обґрунтуйте свою відповідь.
7. (1 бал)  Виписати тільки правильні твердження: 1)два прямокутні рівнобедрених трикутники  з різними площами – це подібні фігури; 2) два квадрати з різними площами завжди подібні; 3)усі  рівносторонні  трикутники з різними периметрами  – це подібні фігури;  4) усі тупокутні трикутники  – це подібні  фігури; 5) усі прямокутники – це подібні фігури; 6) усі різносторонні прямокутні трикутники – це подібні фігури; 7) усі ромби подібні між собою; 8) дві рівнобічні, що мають рівні кути  - це подібні фігури; 9) усі трикутники, що мають рівні відповідні кути, але мають  не рівні периметри – це подібні  фігури.
8. (1 бал)  Висоти  АН1 та СН2 різностороннього DАВС – перетинаються в точці О.    Доведіть, що DАВН1 і DСВН2 є подібними. Чи можна чотирикутник АН2Н1С вважати:  а) трапецією; б) рівнобічною трапецією?
9. (1 бал)  Сторони DАВС а =42 м, b =28 м, c =30 м. Знайдіть  довжини трьох бісектрис DАВС.
10. (1 бал)  Сторони DАВС  а = 18 м, b = 24 м, c = 30 м. Знайдіть  відношення відрізків на трьох бісектрисах, які утворюються точкою перетину бісектрис D АВС.
11. (1 бал)   Сторони DАВС  а = 7 м, b = 24 м, c = 25 м. Знайдіть  радіус кола, вписаного в DАВС.

12. (1 бал)  Хорди кола АВ і СD перетинаються в точці О.  Відомо, що АО:ОВ = 3:4, СО:ОD = 5:1, СО - ОD = 32 м. Знайдіть відрізки, на які точка О розбиває хорди АВ і СD.
Опубліковано о

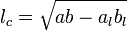
Немає коментарів:

Дописати коментар

Підписатися на: Дописати коментарі (Atom)