Висота́ трику́тника — відрізок, проведений з вершини кута до протилежної сторони або до продовження протилежної сторони і лежить на прямій, перпендикулярній до цієї сторони. Ця сторона називається основою трикутника. Точка перетину сторони і перпендикуляра називається основою перпендикуляра. Довжина висоти — це відстань від вершини до основи трикутника.
Висоту використовують для обчислення площі трикутника: половина добутку довжини висоти на довжину основи дорівнює площі трикутника.
- де h — висота трикутника, опущена на сторону.
В рівнобедреному трикутнику (трикутник в якому дві сторони конгруентні) висота проведена до неконгруентної сторони ділить цю сторону на дві рівні частини. В прямокутному трикутнику висота опущена на гіпотенузу ділить її на два відрізки, нехай це буде p і q. Якщо ми позначимо довжину висоти літерою h то отримаємо співвідношення:
Три висоти перетинаються в одній точці, яка називається ортоцентром трикутника. Ортоцентр лежить всередині трикутника (і відповідно всі основи перпендикулярів лежать в трикутнику) тоді і тільки тоді, якщо трикутник не тупокутний (в ньому жоден з внутрішніх кутів не більший за прямий кут). Дивіться також ортоцентрична система.
Висота трикутника – це перпендикуляр,
проведений з вершини трикутника до прямої, що містить протилежну сторону
трикутника. Трикутник має три висоти, які позначають ha, hb, hc.
Запам’ятайте, з вершини А проходить висота ha, з вершини В опускається висота hb, а з вершини С виходить висота hc.
Зауваження. 1. Прямі що містять висоти
трикутника, перетинаються в одній точці (ортоцентр). У прямокутному трикутнику
ця точка співпадає з вершиною прямого кута, у тупокутному трикутнику ортоцентр
знаходиться зовні трикутника за вершиною тупого кута, в гострокутному
трикутнику ортоцентр знаходиться в середині трикутника ближче до вершина
більшого кута. У прямокутному трикутнику дві висоти співпадають з двома
короткими сторонами(катетами) трикутника, ортоцентр співпадає з вершиною
прямого кута. У тупокутного трикутника дві висоти лежать зовні трикутника, а
третя найкоротша висота лежить всередині трикутника.
Властивості висот трикутника
1. Найбільша висота трикутника проведена до його
найкоротшої сторони, а найменша висота до найдовшої сторони цього трикутника.
2.
Висоти трикутника обернено пропорційні його сторонам
(1/a) :(1/b) :(1/c) =ha:hb :hc
- Кут між висотою та бісектрисою, що
проведені з однієї вершини, рівний піврізниці двох інших кутів цього
трикутника.
- За трьома висотами можна відновити
трикутник.
- Якщо відомими сторонами трикутника можна
обчислити його висоти.
7.Між висотами та
радіусом вписаного кола існує залежність 1/r = 1/ha +1/hb + 1/hc
Практична частина заняття.
Завдання для вироблення умінь та навичок
використовувати властивості
1. Кути трикутника відносяться, як 2:3:4. Розмістити в порядку зростання довжини висот. Чи можуть висоти
перетинатися за межами трикутника?
2. Накресли прямокутний рівнобедрений
трикутник. Проведи в ньому три висоти. Які висоти рівні половині найбільшої сторони трикутника?
Чому?
3. Висота трикутника утворює з прилеглою стороною
кут 89°, а інша висота з протилежною стороною утворює теж кут 1°. Який вид
цього трикутника?
4. Трикутники АВС і МАВ рівні, Чи рівні
відповідні висоти цих трикутників?
5.  АВС=
АВС= КМN,
КМN,  К=90°,
К=90°,  М=60°. Знайди всі кути трикутника АВС, що
утворилися в результаті перетину висот.
М=60°. Знайди всі кути трикутника АВС, що
утворилися в результаті перетину висот.
6. Один з кутів трикутника дорівнює 20°, а
один з двох інших в 4 рази більший другого. Яка найменша висота трикутника.
7. У рівнобедреного трикутника АВС знайди довжини
висот, якщо бічна СВ = 43 м, АВ = 10 м.
9. Кут між висотою і стороною, що проведені з
однієї вершини рівнобедреного трикутника, дорівнює 10°, а один з двох інших
кутів трикутника дорівнює 70°. Знайди усі невідомі кути в середині трикутника, що
утворилися в результаті перетину висот.
10. Знайди вид прямокутного трикутника, якщо у
нього є дві рівні висоти.
11. Обчислити довжини висот трикутника, знаючи, сторони трикутника:
1) 2, 8, 4; 2) 4, 3, 5; 3) 2, 3, 5;, 4) 2, 7, 3; б) 8, б, 5. Знайти довжини відрізків,
на які ділиться кожна сторона трикутника висотою.
12. Скільки рівних висот у тупокутного різностороннього
трикутника. Накресліть будь-який тупокутний різносторонній трикутник та точку
перетину висот.
13. Висота, що проведена до основи
рівнобедреного трикутника нахилена до його основи під кутом ..... . Знайти види
таких трикутників. Скільки розв’язків має задача?
14. У трикутника три рівні висоти. Який вид
цього трикутника?
15. У трикутника висота ділить сторону навпіл . Чи може цей трикутник бути
прямокутним?( Тупокутним? Гострокутним?)
16. Периметр рівнобедреного трикутника 18 см,
бічна сторона на 3 см довша від основи.
Знайти висоти цього трикутника.
Завдання для самостійного закріплення умінь
та навичок досліджувати та аналізувати навчальний матеріал
1.Якого виду трикутник можна утворити, маючи три висоти
рівностороннього (рівнобедреного та
різностороннього) трикутника?
2.На скільки тупокутних трикутників можуть
поділити прямокутний трикутник дві його висоти?
3.Чи завжди будь-які три відрізки можуть бути висотами
трикутника?
4.Чи відповідні висоти нерівних трикутників
можуть виявитися рівними?
5.Відновити на довільному тупокутному
трикутнику висоти стандартного трикутника. Виміряти їх та знайти суму їх,
порівняти з периметром трикутника.
6. Визначити довжини висот трикутників, у яких
величини сторін: а)46м, 46м, 19м. б)35м,35м,35м. в) 7м, 7м, 9м?
7.Скільки тупокутних трикутників можна
утворити висотами рівностороннього трикутника?
8.Чи
існують трикутники, у яких до найменшої сторони проведена найменша за довжиною висота?
9.Яка середня за величиною висота в трикутнику
АВС, якщо:
1) а =
51 см; b =36 cм, с = 47 см?
2) а = 68
см; b = 56 cм, с = 58 см?
3) а = 5
см; b = 8 cм, с = 7 см?
4) а = 58 см; b = 58 cм, с = 59 см?
5) а = 5 см; b = 5 cм, с = 5 см?
Запишіть висоти в порядку спадання. Знайти
довжини сторін, на які ділиться кожна сторона трикутника висотою.
10. З ЯКОГО КУТА ПРОВЕДЕНА найбільша висота в трикутнику АВС, якщо
1)  350
,
350
,  780?
780?
1)  450
,
450
,  1300 ?
1300 ?
1)  740 ,
740 ,  590?
590?
1)  970 ,
970 ,  180?
180?
1)  450
,
450
,  670
?
670
?
1)  720,
720,
 780?
780?
Запишіть висоти цих трикутників у порядку
зростання, не шукаючи їх довжини.
Задачі для самостійних дослідів учнів.
1.Чи існує вид прямокутного трикутника, щоб
довжина його найменшої сторони була рівна довжині висоти, що проведена до
найбільшої сторони?
2.Які існують види трикутників , у яких усі висоти різні? Замалювати
кожний можливий випадок.
Фронтальне опитування
Які основні властивості висот трикутника ми вивчаємо
напам’ять? Як їх формулюють? Які властивості співвідношень у сторін та висот
трикутника?

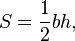
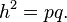










Немає коментарів:
Дописати коментар