Тригонометрія в прямокутному трикутнику
Тригонометричні функції для гострих кутів можна визначити як відношення сторін прямокутного трикутника. Для будь-якого даного кута можна побудувати прямокутний трикутник, що містить такий кут, і зі сторонами: протилежним катетом, прилеглим катетом і гіпотенузою, пов'язаними з цим кутом певним співвідношенням. Ці відносини сторін не залежать від конкретного обраного прямокутного трикутника, а залежать тільки від заданого кута, так як всі трикутники, побудовані таким чином, є подібними.
- Синусом гострого кута прямокутного трикутника називається відношення протилежного катета до гіпотенузи.
- Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи.
- Тангенсом гострого кута прямокутного трикутника називається відношення протилежного катета до прилеглого катета.
- Котангенсом гострого кута прямокутного трикутника називається відношення прилеглого катета до протилежного катета.
Розглянемо у формальних позначених через малюнок вище.
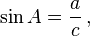 звідси
звідси 
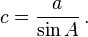
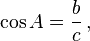 звідси
звідси 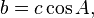

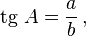 звідси
звідси 
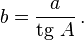
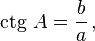 звідси
звідси 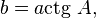
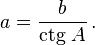
Звідси можна зробити висновок, що:
- Щоб знайти катет, протилежний до гострого кута прямокутного трикутника, потрібно гіпотенузу помножити на синус цього кута, або прилеглий катет помножити на тангенс цього кута.
- Щоб знайти катет, прилеглий до гострого кута прямокутного трикутника, потрібно гіпотенузу помножити на косинус цього кута, або протилежний катет помножити на котангенс цього кута.
- Щоб знайти гіпотенузу, потрібно катет, прилеглий до гострого кута, поділити на косинус цього кута, або катет, протилежний до гострого кута, поділити на синус цього кута.
Завдання для самостійного опрацювання
Варіант 1.
1. У прямокутного DАВС(<С = 90о, <В= 60о) виразити через відношення сторін такі тригонометричні величини:
sin<В =?, sin <A=?, cos <В=? , cos<A=?, tg<В=? , tg<A=? , ctg<В=? , ctg<A=?
2. Використовуючи трійку сторін (а; b; с) прямокутного DАВС(<С = 90о) знайти числові значення тригонометричних виразів: sin<В =?, sin<A=?, cos <В=? , cos<A=?, tg<В=? , tg<A=? , ctg<В=? , ctg<A=? якщо: 1)( 9; 40; 41); 2) (189; 340; 380); 3) (21; 20; 29); 4) (7; 24; 25) ; 5) (45; 28; 53); 6) (21; 220; 221); 7) (13; 84; 85); 8) (65; 72; 97); 9)( 69; 260; 269); 10) (165; 52; 173); 11) (57; 176; 185); 12) (88; 105; 137); 13) (77; 36; 85); 14) (45; 28; 53); 15) (33; 56; 65); 16) (11, 60, 61).
3. Використовуючи трійку сторін (а; b; с) прямокутного DАВС(<С = 90о) знайти числові значення тригонометричних виразів: sin<В =?, sin <A=?, cos <В=? , cos<A=?, tg<В=? , tg<A=? , ctg<В=? , ctgÐ<A=? якщо є тільки дві відомі сторони: 1)( 15; 8; с); 2) (35; 12; с); 3) (а; 12; 13); 4) (а; 24; 25); 5) (45; b; 53); 6) (33; b; 65); 7) (а; 84; 85); 8) (63; 16; с); 9)(а; 112; 113); 10) (165; b; 173); 11) (а; 260; 269); 12) (312; b; 313).
4. Виписати тільки правильні твердження для прямокутного DАВС(<С = 90о, СН -висота): 1)sin <В = СА/AB; 2) sin <A=CB/AB; 3) cos <В= CB/AB; 4) cos<A = СА/AB; 5) tg<В =CA/CB; 6) tg<A = CB/AC; 7)ctg<В = CB/AC; 8)сtg<A = CA/CB; 9)sin <В = СН/ВС; 10) sin <A=CН/AС; 11) cos <В = НB/СB; 12)cos<A = НА/AС; 13) tg<В =CН/НB; 14) tg<A = CН/AН; 15)ctg<В = НB/НC; ,16)ctg<A = НA/CН.
5. Знайти катет АС прямокутного DАВС(<С = 90о, <В= 60о) з гіпотенузою, що рівна: 1)8м; 2) 12 см; 3) 4 км; 4) 24 см; 5) 44м; 6) 33 см; 7) 84 см; 8) 16 см; 9) 11 см; 10) 13 см; 11) 26 см; 12) b см.
6. Знайти катет ВС прямокутного DАВС(<С = 90о, <В= 30о) з гіпотенузою, що рівна: 1)8м; 2) 12 см; 3)1 км; 4) 24 см; 5) 44м; 6) 33 см; 7) 84 см; 8) 16 см; 9) 11 см; 10) 13 см; 11) 26 см; 12) n см.
7. Знайти гіпотенузу АВ прямокутного DАВС(<С = 90о, <В= 45о) з катетом, що рівний: 1)8м; 2) 12 см; 3)1 км; 4) 24 см; 5) 44м; 6) 33 см; 7) 84 см; 8) 16 см; 9) 11 см; 10) 13 см; 11) 26 см; 12) k см.
8. Знайти катет ВС прямокутного DАВС(<С = 90о, <В= 60о) з катетом АС, що рівний: 1)8м; 2) 12 см; 3)1 км; 4) 24 см; 5) 44м; 6) 33 см; 7) 84 см; 8) 16 см; 9) 11 см; 10) 13 см; 11) 26 см; 12) b см.
Варіант 2.
1. У прямокутного DАВС(<С = 90о) з катетом СВ= 8 см і провели найменшу висоту СН = 4 см. Знайти градусну міру усіх гострих кутів трикутника СВН . Не забудьте використати таблиці тригонометричних величин(таблиці Брадіса).
2. Знайти значення виразів: sin45о =?, sin60о=?, cos30о=?, cos60о=?, tg30о =? , tg60о =?, ctg60о =?, ctg30о =?, ctg45о=?
3. Знайти градусні міри гострих кутів, використовуючи тригонометричні таблиці Брадіса, і знаючи сторони (а; b; с) прямокутного DАВС(<С = 90о), якщо: 1)( 9; 40; 41); 2) (189; 340; 380); 3) (21; 20; 29); 4) (7; 24; 25) ; 5) (45; 28; 53); 6) (21; 220; 221); 7) (13; 84; 85); 8) (65; 72; 97); 9)( 69; 260; 269); 10) (165; 52; 173); 11) (57; 176; 185); 12) (88; 105; 137); 13) (77; 36; 85); 14) (45; 28; 53); 15) (33; 56; 65); 16) (11, 60, 61).
4. Знайти градусні міри гострих кутів, використовуючи тригонометричні таблиці Брадіса, і сторони (а; b; с) прямокутного DАВС(<С = 90о), якщо є дві відомі сторони: 1)( 15; 8; с); 2) (35; 12; с); 3) (а; 12; 13); 4) (а; 24; 25); 5) (45; b; 53); 6) (33; b; 65); 7) (а; 84; 85); 8) (63; 16; с); 9)(а; 112; 113); 10) (165; b; 173); 11) (а; 260; 269).
5. Виписати тільки правильні твердження для прямокутного DАВС(<С = 90о, СН -висота): 1)АН2 + ВС2 = ВА2;
2) НВ2 + НС2 = СА2; 3) НВ2 - ВС2 = НА2; 4) НВ2 - НС2 = СВ2; 5) НВ2 - АС2 = АВ2; 6)СН2 = ВН∙НА; 7) СВ2 = ВН∙ВА; 8)СА2 = ВА∙НА; 9) СН2 = ВА∙СА; 10) СВ2 - НС2 = НВ2; 11) СА2 - НС2 = НА2; 12) СН2 + НВ2 = СВ2; 13) СН2 + НА2 = СА2.
6. Знайти кут при вершині рівнобедреного трикутника зі сторонами: : 1)( 18; 41; 41); 2) (378; 380; 380); 3) (42; 29; 29); 4) (14; 25; 25) ; 5) (90; 53; 53); 6) (42; 221; 221); 7) (26; 85; 85); 8) (130; 97; 97); 9)( 138; 269; 269); 10) (230; 173; 173); 11) (114; 185; 185); 12) (176; 137; 137); 13) (154; 85; 85); 14) (10; 13; 13); 15) (66; 65; 65); 16) (22, 61, 61).
7. Знайти кути при основі рівнобедреного трикутника з відомою основою та відомою бічною стороною: 1)8м і 5 см; 2) 10 см і 25 см; 3) 10см і 13см; 4) 66см і 65см; 5)22см і 61см; 6)42см і 29см; 7) 14м і 25м; 8) 90см і 53см.
8. Катети прямокутного DАВС(<С = 90о) відносяться, як: 1)8:15; 2)35:12;3)16:63;4)20:99; 5)12:5; 6)55:48; 7) 11:60; 8) 9:40. Медіана СМ рівна: 1) 34 см; 2)74м;3)130м; 4)202м; 5)26м; 6)146м; 7)122м; 8) 82м. Знайти а та Ðb DАВС.
8. У прямокутному DАВС(<С = 90о) медіана і висота, проведені з вершини прямого кута, 25 і 24 см. Знайдіть гострі кути прямокутного DАВС.
Варіант 3.
1. Виписати у відповідь тільки правильні тригонометричні тотoжності: 1) sin2b + cos2b = 1; 2)ctgb ∙tgb =1;
3) ctgb =(sin b) / ( cosb) ; 4) tga=(sin a) / (cosa); 5) ctg2b +1/ sin2b =1; 6) ctga∙ tgb =1; 7) tg2a+1/cos 2a=1;
8)sin210o + cos210o =1, 9) (cos4o)/( cos4o)=1, 10)tg2a∙c tg2a=1; 11)ctga∙tga=1; 12) sin2a+ cos2a = 1.
2. Спростити тригонометричні вирази: 1) (sing +cosg)2 / (1+2sing ∙cosg) ; 2) cosa∙tga + (sin2a)/( tg2a);
3) sin2b +cos2b - tg2a∙c tg2a; 4) sin4a -cos4a; 5) tga∙ sina - 1/(cosa); 6) ctg2a+1/(sin2g) - 1; 7) -1+tg2a+1/cos 2a ;
3. Знайти: 1) cos2(90o -10o ) + cos210o = ?; 2) sin2(90o -40o ) + sin240o = ?; 3)sin(90o -40o) /cos40o) = ?.
4. Чому дорівнює sina, ctga, tga, якщо соsa = 0,6? 5. Чому дорівнює соsa, ctga, tga, якщо sina = 0,8?
6. У прямокутному трикутнику відомо: а)катет і гострий кут; б)гіпотенуза і гострий кут. Знайти невідомі сторони.
Тригонометрія в прямокутному трикутнику
Розглянемо прямокутний трикутник АВС, кут С ‒ прямий. Позначимо за α кут А. Косинусом гострого кута прямокутного трикутника називається відношення довжин прилеглого катета та гіпотенузи: cos l =АС/АВ. Синусом гострого кута прямокутного трикутника називається відношення довжин протилежного катета та гіпотенузи: sin l = ВС/АВ. Тангенсом гострого кута прямокутного трикутника називається відношення довжин протилежного та прилеглого катетів: tg l= ВС/АС. Котангенсом гострого кута прямокутного трикутника називається відношення довжин прилеглого та протилежного катетів: ctg l= АВ/ВС.
Довідник з геометрії РІВНОСТРОННЬОГО ТА ПРЯМОКУТНОГО трикутника
Прямокутний трикутник — трикутник, один із кутів якого прямий. Прямокутний трикутник займає особливе місце в планіметрії, оскільки для нього існують прості співвідношення між сторонами і кутами.
Сторони прямокутного трикутника мають власні назви. Дві сторони, що утворюють прямий кут називаються катетами, а третя сторона — гіпотенузою. Традиційно катети позначаються літерамиa та b, а гіпотенуза — літерою c. За теоремою Піфагора можна знайти будь-яку сторону прямокутного трикутника, якщо відомі дві інші сторони. За цією теоремою квадрат гіпотенузи дорівнює сумі квадратів катетів.
Звідси можна знайти інші сторони прямокутного трикутника.
Катети є водночас висотами прямокутного трикутника. Тому площа прямокутного трикутника дорівнює:
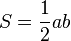 .
.
Деякі властивості прямокутних трикутників
- Сума гострих кутів прямокутного трикутника дорівнює 90°.
- Якщо у прямокутному трикутнику один з гострих кутів дорівнює 30°, то катет протилежній цьому куту буде дорівнювати половині гіпотенузі.
- Якщо катет прямокутного трикутника дорівнює половині гіпотенузи, то кут, що лежить проти цього катета, дорівнює 30°.
- Медіана, проведена до гіпотенузи прямокутного трикутника, ділить його на два рівнобедрених трикутника, оскільки медіана дорівнює половині гіпотенузи.
- Якщо описати коло навколо прямокутного трикутника, то гіпотенуза буде діаметром кола.
Ознаки рівності прямокутних трикутників
У прямокутного трикутника є чотири ознаки рівності:
- За двома катетами.
Якщо катети одного прямокутного трикутника дорівнюють відповідно катетам другого трикутника, то такі трикутники рівні.
- За катетом і гострим кутом.
Якщо катет і гострий кут одного прямокутного трикутника дорівнюють відповідно катету й гострому куту другого трикутника, то такі трикутники рівні.
- За гіпотенузою і катетом.
Якщо гіпотенуза і катет одного прямокутного трикутника дорівнюють відповідно гіпотенузі й катету другого трикутника, то такі трикутники рівні.
- За гіпотенузою і гострим кутом.
Якщо гіпотенуза і гострий кут одного прямокутного трикутника дорівнюють відповідно гіпотенузі й гострому куту другого трикутника, то такі трикутники рівні.
Вписане й описане коло прямокутного трикутнику
Описане коло[ред. • ред. код]
Центром кола, описаного навколо прямокутного трикутника, є середина гіпотенузи. Нехай  — центр описаного кола навколо прямокутного
— центр описаного кола навколо прямокутного  ABC:
ABC:
 — центр описаного кола навколо прямокутного
— центр описаного кола навколо прямокутного Вписане коло[ред. • ред. код]
У прямокутний трикутник  ABC з прямим кутом
ABC з прямим кутом 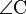 вписане коло, яке дотикається до катетів у точках
вписане коло, яке дотикається до катетів у точках  і
і  . Відрізки
. Відрізки  і
і 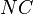 дорівнюють радіусу кола.
дорівнюють радіусу кола.
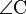 вписане коло, яке дотикається до катетів у точках
вписане коло, яке дотикається до катетів у точках  і
і  . Відрізки
. Відрізки  і
і 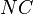 дорівнюють радіусу кола.
дорівнюють радіусу кола.
Радіус вписаного кола у прямокутний трикутник з катетами  і
і  і гіпотенузою
і гіпотенузою  знаходиться за формулою:
знаходиться за формулою:
 і
і  і гіпотенузою
і гіпотенузою  знаходиться за формулою:
знаходиться за формулою:
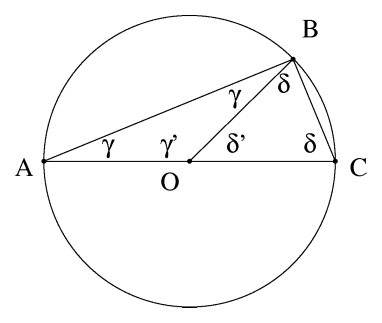
В геометрії, Теорема Фалеса (названа на честь Фалеса з Мілету) стверджує, що якщо A, B і C є точками на колі, де відрізок AC є діаметром кола, тоді кут ABC є прямим.
Теорема Фалеса є окремим випадком теореми про вписані кути. Вона згадується і доводиться як 33-я пропозиція, третьої книги Евкліда «Начала».
Доведення
Використаємо такі факти: сума кутів трикутника дорівнює двом прямим кутам і що кути при основі рівнобедреного трикутника рівні.
Нехай O є центром кола. Оскільки OA = OB = OC, OAB і OBC є рівнобедреними трикутниками, із рівності кутів при основі рівнобедреного трикутника, OBC = OCB і BAO = ABO. Нехай γ = BAO і δ = OBC.
Оскільки сума кутів прямокутного трикутника рівна двом прямим кутам, отримаємо
- 2γ + γ ′ = 180°
і
- 2δ + δ ′ = 180°
Також відомо що
- γ ′ + δ ′ = 180°
Додавши перші два рівняння та віднявши третє, отримаємо
- 2γ + γ ′ + 2δ + δ ′ − (γ ′ + δ ′) = 180°
що, після скорочення γ ′ and δ ′, дає
- γ + δ = 90°
Обернена теорема
Обернена теорема також вірна. Вона стверджує, що якщо для даного прямокутного трикутника побудувати коло, так, що його гіпотенуза буде діаметром кола, то коло буде описаним навколо трикутника.
Пряма та обернена теореми можуть бути сформульовані так:
- Центр описаного навколо трикутника кола лежить на одній із його сторін тоді і тільки тоді, коли трикутник є прямокутним.
Узагальнення
Теорема Фалеса є спеціальним випадком наступної теореми: якщо дані три точки A, B і C на колі із центром O, кут AOC вдвічі більшим від ABC.
Історія
Фалес не був першовідкривачем теореми названої в його честь, оскільки давні єгиптяни та вавілоняни знали її на емпіричному рівні. Але Фалесу належить перше доведення цієї теореми.
Висота
Квадрат висоти прямокутного трикутника, проведеної до гіпотенузи, дорівнює добутку проекцій катетів на гіпотенузу.
Квадрат катета дорівнює добутку гіпотенузи і проекції цього катета на гіпотенузу.
де a, b, c, d, e, f такі, як позначено на малюнку. Тоді висоту можна записати через сторони трикутника:
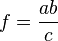 або через катети
або через катети
Розв’язування рівностороннього трикутника
| ||||||||||||||||
a
|
(2h∙30,5):3
|
Р/3
|
2p/3
|
R∙30,5
|
2r∙30,5
|
2/3(3S∙30,5)0,5
| ||||||||||
h
|
(a∙30,5)/2
|
(P∙30,5)/6
|
(p∙30,5)/3
|
3r/2
|
3r
|
(S∙30,5)0,5
| ||||||||||
P
|
3a
|
2h∙30,5
|
2p
|
3R∙30,5
|
6r∙30,5
|
2(3S∙30,5)0,5
| ||||||||||
p
|
3a/2
|
h30,5∙
|
p/2
|
(r∙30,5)/2
|
3r∙30,5
|
(3S∙30,5)0,5
| ||||||||||
R
|
(a∙35)/3
|
2h/3
|
(P∙30,5)/9
|
(2p∙30,5)/9
|
2r
|
2/3 ∙(S∙30,5)0,5
| ||||||||||
r
|
(а∙30,5)/6
|
h/3
|
P∙30,5/18
|
(P∙3)0,5/18
|
R/2
|
((S∙30,5)0,5)/3
| ||||||||||
S
|
(a2∙30,5)/4
|
(h2∙30,5)/3
|
(P2∙30,5)/36
|
(р2∙30,5)/9
|
(3R2∙30,5)
|
3r2∙30,5
| ||||||||||
Розв’язування прямокутного трикутника з кутами ÐС=90о, ÐА=30о с =
| ||||||||||||||||
a= 0,5c
|
b=30,5/2
|
b=30,5∙a
|
S=0,5∙30,5∙a2
|
S=30,5∙b2/6
|
S=30,5∙c2/8
|
S= r2+2Rr
| ||||||||||
Площа прямокутного трикутника(а і b катети)
| ||||||||||||||||
S=0,5ab
|
S=0,5a2 tgβ
|
S=0,5a2ctgα
|
S=0,5b2tgα
|
S=0,5b2ctgβ
|
S=0,25c2sin2α
|
S=0,25c2sin2β
| ||||||||||
Знаходження сторін прямокутного трикутника(а і b катети): с =
| ||||||||||||||||
а = с∙sinα
|
а = с∙cosβ
|
а = b∙ctgβ
|
а = b∙tgα
|
b = с∙sinβ
|
b = с∙cosα
|
b = a∙tgβ = a∙ctgα
| ||||||||||
Рівнобедрений прямокутний трикутник: а= b; ÐС=90о, ÐА=45о; ÐВ=45о; с=
| ||||||||||||||||
b= a =20,5c; ha = hb = a =b; ma= mb=0,5∙50,5∙a; mc= hb= lc= 0,5∙c; S = 0,5∙a2 = 0,25c2
| ||||||||||||||||
Прямокутний трикутник. Медіани, висоти, радіус вписаного кола.
| ||||||||||||||||
mc= 0,5c; r = p – c; ma = 0,5(4b2+a2)0,5; mb = 0,5(4a2+b2)0,5; ma2+mb2 = 5mc2;
r = ab/(a+b+c); a = (c∙ac)0,5; b = (c∙bc)0,5; hc = (ac∙bc)0,5; hc = a∙b/c; hc = a∙b/(ac +bc);
r = (a+b-c)/2;
| ||||||||||||||||
1.У прямокутному трикутнику з гострим кутом 300 бісектриса середнього кута ділить середню сторону у відношенні 1:2 починаючи від вершини прямого кута.
2.У прямокутному трикутнику з гострим кутом 300 найменша висота рівна половині більшого катета.
3.У прямокутному трикутнику з гострим кутом 750 найменша висота рівна чверті гіпотенузи.
4.У прямокутному трикутнику з гострим кутом 750 найменша висота рівна половині радіуса описаного кола.
5.У прямокутному трикутнику з гострим кутом 150 найменша квадрат найменшої висоти рівний половині площі трикутника.
6.У прямокутному трикутнику з гострим кутом 600 кожна сторона поділена точкою на дві частини у відношенні 1:2, починаючи з вершини більшого кута. Ці три точки поділу сторін утворюють правильний трикутник, площа якого становить дві дев’ятих площі прямокутного трикутника. Ці три точки поділу сторін є точками дотику вписаного кола в даний прямокутний трикутник.
7.У прямокутному трикутнику з гострим кутом 600 найменша висота ділить бісектрису середнього кута навпіл.
8.У прямокутному трикутнику з гострим кутом 600 найменша медіана перпендикулярна до бісектриси середнього кута.
9.У прямокутному трикутнику з гострим кутом 600 бісектриса середнього кута ділить навпіл найменшу медіану.
10. У прямокутному трикутнику найменша медіана ділить навпіл площу цього трикутника.
11. У прямокутному трикутнику сторони можуть виражатися натуральними числами за формулами:
а = m2 – n2; b = 2mn; c = m2 + n2 .
m/n
|
2
|
4
|
6
|
8
|
10
|
12
|
1
|
3, 4, 5
|
15, 8,17
|
35,12,37
|
63,16,65
|
99,20,101
|
143,24,145
|
3
|
5,12,13.
|
7, 24.25
|
-------------
|
55.48.73
|
91.60,109
|
--------------
|
5
|
21.20.29
|
9.40.41
|
11, 60, 61
|
38, 80, 89
|
-------------
|
169,120,119
|
7
|
45.28.53
|
33.56.65
|
13.84.85
|
15.112.113
|
51.140.149
|
95.169.193
|
9
|
77.36.85
|
65.72.97
|
------------
|
17.144.145
|
19.180.181
|
-------------
|
11
|
44.117.125
|
88.105.137
|
85.132.157
|
57.176.185
|
21.220.221
|
23.264.265
|
13
|
52.165.173
|
104.153.135
|
133.156.175
|
105.208.233
|
69.260.269
|
25.312.313
|
15
|
60.221.229
|
120.209.241
|
-----------
|
161.240.289
|
-------------
|
--------------
|
17
|
68.285.293
|
136.273.305
|
204.253.325
|
225.273.353
|
189.340.380
|
145.408.433
|
19
|
76.357.365
|
152.345.377
|
228.325.397
|
297.304.425
|
261.380.461
|
217.456.505
|
21
|
84.437.445
|
168.425.457
|
------------
|
366.377.505
|
341.420.541
|
--------------
|
23
|
92.525.533
|
184.513.540
|
276.493.565
|
368.468.593
|
429.460.629
|
385.552.673
|
25
|
100.621.629
|
200.609.641
|
589.300.661
|
400.561.689
|
-------------
|
481.600.769
|
Тригонометрія на прямокутному трикутнику
Розглянемо прямокутний трикутник АВС, кут С ‒ прямий. Позначимо за α кут А. Косинусом гострого кута прямокутного трикутника називається відношення довжин прилеглого катета та гіпотенузи: cos l =АС/АВ. Синусом гострого кута прямокутного трикутника називається відношення довжин протилежного катета та гіпотенузи: sin l = ВС/АВ. Тангенсом гострого кута прямокутного трикутника називається відношення довжин протилежного та прилеглого катетів: tg l= ВС/АС. Котангенсом гострого кута прямокутного трикутника називається відношення довжин прилеглого та протилежного катетів: ctg l= АВ/ВС.
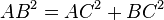
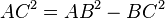
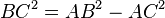

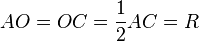

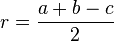


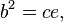
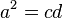
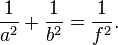
Немає коментарів:
Дописати коментар