Ромби, що вписані в трикутник

         

Ромби, що  вписані в трикутник

Означення. Ромб називається вписаним в трикутник, якщо усі чотири вершини лежать на сторонах трикутника або на їх продовженнях.

Класифікація. Існують по-різному вписані ромби в довільний трикутник.  Деякі внутрішні області вписаних ромбів повністю належать внутрішній області трикутника, а в інших вписаних ромбах тільки частина внутрішньої області належить внутрішній області трикутника.

Окремі випадки вписаних ромбів в трикутник.

Наводимо приклад вписаного ромба в трикутник,  дві сторони  якого мають спільну вершину  і лежать на сторонах  даного трикутника АВС з відомими сторонами а, b, с.  У цьому  випадку кут А ромба AKLM – рівний куту трикутника CAB. За властивістю діагоналей ромба, діагональ AL ромба співпадає з бісектрисою трикутника AL = l_a. Саме на цій бісектрисі, як на діагоналі ромба отримаємо вписаний ромб. Згідно властивостям бісектриси трикутника та подібності трьох трикутників АВС, LCK, MLB  можна за відомим сторонами трикутника обчислити усі відрізки, що є в трикутнику АВС та сторону ромба. Звертаємо увагу на те, що кожна бісектриса трикутника визначає вписаний ромб в даний трикутник. Такі вписані ромби в трикутник назвемо бісектрально вписані ромби. Зрозуміло, що довільний трикутник має три бісектрально вписаних ромби. Кожна сторона бісектрально вписаних ромбів в трикутник паралельна сторонам трикутника, і існує  тільки один кут ромба, що суміщається з кутом трикутника.

В довільний трикутник ще можна вписати ромб по-іншому, тобто, цей ромб не буде бісектрально вписаний в трикутник, і вершини його будуть лежати на сторонах трикутника. Виконаємо побудову небісектрально вписаного ромба.  Накреслимо відрізок КМ. Пряма КМ розбиває площину на дві півплощині p₁  та  p₂.  Будемо вважати довжину відрізка КМ рівну стороні  ромба та задамо висоту ромба h, тоді на  площині  відрізок МК визначає   чотири рівні ромби. По одну сторону від відрізка МК(нехай це буде півплощина p₁) за допомогою циркуля і лінійки  побудуємо  два ромба КММ₂К₂  і КММ₁К₁, а по іншу сторону від МК (це буде півплощина p₂ ) задаємо вершину  В трикутника АВС. 

Навколо цих двох ромбів можна описати  безліч трикутників А_nВ_nС_n , де n – натуральне число. Для цього достатньо у півплощині p₂  задавати  довільну точку, як вершину В_n   і з’єднувати цю точку з кінцями відрізка КМ.  Перетин прямих В_nК та  В_nМ з прямою  М₁К₁ утворюють дві вершини А_n та С_n трикутника А_nВ_nС_n. 

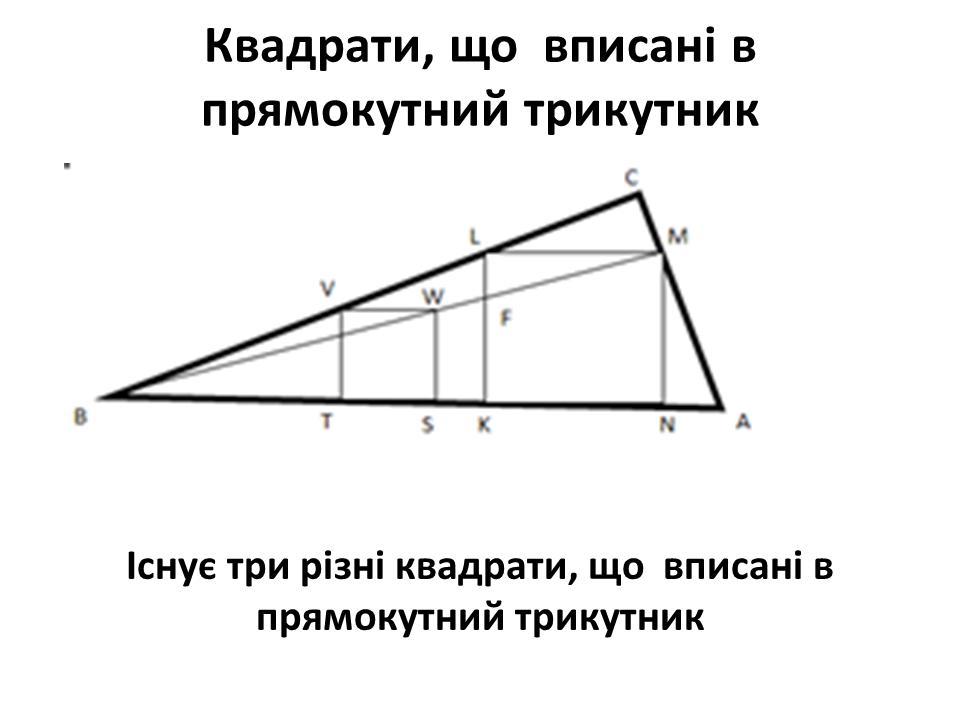
Квадрати, що  вписані в прямокутний трикутник

Означення. Квадрат називається вписаним в прямокутний трикутник, якщо усі чотири вершини лежать на сторонах прямокутного трикутника.

Класифікація. Існує два різні квадрати, що вписані в довільний прямокутний трикутник.  

В одного вписаного квадрата дві вершини лежать на гіпотенузі,  а в іншого вписаного квадрата  одна вершина  лежить на гіпотенузі.

Побудова  квадратів, що вписані в прямокутний трикутник

1. Побудуємо квадрат KLMN, вписаний в прямокутний трикутник ABC , дві вершини якого лежать на гіпотенузі, використовуючи гомотетію.  Для цього спочатку на катету ВС візьмемо точку V так, щоб виконувалась умова:  

BV ≤ 0,5BC.

З точки V опустимо перпендикуляр на гіпотенузу АВ, отримаємо основу перепендикуляра точку Т.  Тобто  VТ ^АВ.  На гіпотенузі АВ відкладемо від точки Т  відрізок TS, що рівний перпендикуляру VT. На двох перпендикулярних і рівних  відрізках TS i VT побудуємо квадрат VTSW.  Використовуючи гомотетію з центром в точці  В  в напрямі   прямої ВW отримає точку М, яка є точкою перетину катета СА та прямої ВW. Аналогічно скористаємося перетворенням  цієї гомотетії  для трьох інших точок квадрату VTSW та  отримаємо квадрат  KLMN, вписаний в прямокутний трикутник ABC.

2. Побудуємо квадрат KLMС, вписаний в прямокутний трикутник ABC , одна вершина  якого лежить на гіпотенузі. використовуючи гомотетію.  Для цього спочатку на катету АС візьмемо точку V так, щоб виконувалась умова:  

СV ≤ 0,5АC.

  На катеті СВ відкладемо від точки С  відрізок CW, що рівний відрізку VC.  Тобто  VС ^ CW. На двох перпендикулярних і рівних  відрізках VС  і CW побудуємо квадрат СWSV.  Використовуючи гомотетію з центром в точці  C  в напрямі   прямої CS отримає точку L, яка є точкою перетину гіпотенузи  ВА та прямої CS.  Аналогічно скористаємося перетворенням  цієї гомотетії  для трьох інших точок квадрату СWSV  та  отримаємо квадрат  KLMС, вписаний в прямокутний трикутник ABC.

Знайдемо сторону квадрата KLMС.  Розглянемо бісектрису СL, що проведена на гіпотенузу трикутника CAB  і утворює з катетами  трикутника CAB  кути, що рівні  45°.

Властивості квадратів, що вписані в прямокутний трикутник.

1.  Площа вписаного квадрата, одна вершина якого  лежить на гіпотенузі,  строго більша, ніж площа вписаного квадрата, дві вершини  якого  лежить на гіпотенузі .

2. Діагональ вписаного  квадрата, одна вершина якого  лежить на гіпотенузі, являється  бісектрисою прямого  кута  прямокутного трикутника.

3. Якщо тільки одна вершина вписаного  квадрата лежить на гіпотенузі, то вона поділяє гіпотенузу   прямокутного трикутника на відрізки:  aс:(b+a) та  bс:(b+a),  починаючи від вершини гострого кута А.

Задача 1. Квадрат KLMN вписаний в прямокутний трикутник ABC ( <С = 90°) з відомими катетами  a, b так, що дві вершини L  i  M лежать на катетах ВС та СА відповідно. Знайти сторону квадрата KLMN.

Розв’язання.

Нехай  дано прямокутний трикутник ABC (<С = 90°) з відомими катетами  a = BC, b = AC. Згідно теореми Піфагора маємо, довжину гіпотенузи:  с =  (b² + а²) ^0,5. Побудуємо квадрат KLMN, вписаний в прямокутний трикутник ABC , використовуючи гомотетію.  Для цього спочатку на катету ВС візьмемо точку V так, щоб виконувалась умова:  

BV ≤ 0,5BC.

З точки V опустимо перпендикуляр на гіпотенузу АВ, отримаємо основу перепендикуляра точку Т.  Тобто  VТ ^АВ.  На гіпотенузі АВ відкладемо від точки Т  відрізок TS, що рівний перпендикуляру VT. На двох перпендикулярних і рівних  відрізках TS i VT побудуємо квадрат VTSW.  Використовуючи гомотетію з центром в точці  В  в напрямі   прямої ВW отримає точку М, яка є точкою перетину катета СА та прямої ВW. Аналогічно скористаємося перетворенням  цієї гомотетії  для трьох інших точок квадрату VTSW та  отримаємо квадрат  KLMN, вписаний в прямокутний трикутник ABC.

Знайдемо сторону квадрата KLMN.  Розглянемо три подібних  між собою трикутники: CML, NAM,  CAB.  Для складання пропорцій для сторін подібних трикутників введемо позначення відрізків: CL = у,  ВL = а-у, CM = х,  МА = b – х, ML = LK = KN = MN = z.  Із подібності трикутників CML, CAB  маємо рівність

z² = у(b – х).                             (1)

Із подібності трикутників CML, CAB  маємо рівність

у = ах/ b.                                 (2)

Для прямокутного  CAB  маємо рівність

z² = у² + х².                               (3)

Рівності    (1), (2), (3) утворюють  систему рівнянь з невідомими (х;у; z ).  Розв’язуючи способом підстановки цю систему, отримаємо розв’язок системи, що задовільняє умову задачі(не задовільняє умову тривіальний ров’язок системи (0;0;0)):

х = a²b / (c²+ ba);

у = ab² / (c²+ ba);

z = abc / (c²+ ba).

Таким чином,  ML = LK = KN = MN = z = abc / (c²+ ba),  де с =  (b² + а²) ^0,5.

Відповідь:  abc:(c²+ ba) одиниць довжини, де с =  (b² + а²) ^0,5.

Задача 2.  Квадрат KLMС вписаний в прямокутний трикутник ABC (<С = 90°) з відомими катетами  a, b так, що дві сторони KС  i  СM лежать на катетах ВС та СА відповідно, а одна вершина  цього квадрата лежить на гіпотенузі . Знайти сторону квадрата KLMС.

Розв’язання.

Нехай  дано прямокутний трикутник ABC (<С = 90°) з відомими катетами  a = BC, b = AC. Згідно теореми Піфагора маємо, довжину гіпотенузи:  с =  (b² + а²) ^0,5. Побудуємо квадрат KLMС, вписаний в прямокутний трикутник ABC , використовуючи гомотетію.  Для цього спочатку на катету АС візьмемо точку V так, щоб виконувалась умова:  

СV ≤ 0,5АC.

  На катеті СВ відкладемо від точки С  відрізок CW, що рівний відрізку VC.  Тобто  VС ^ CW. На двох перпендикулярних і рівних  відрізках VС  і CW побудуємо квадрат СWSV.  Використовуючи гомотетію з центром в точці  C  в напрямі   прямої CS отримає точку L, яка є точкою перетину гіпотенузи  ВА та прямої CS.  Аналогічно скористаємося перетворенням  цієї гомотетії  для трьох інших точок квадрату СWSV  та  отримаємо квадрат  KLMС, вписаний в прямокутний трикутник ABC.

Знайдемо сторону квадрата KLMС.  Розглянемо бісектрису СL, що проведена на гіпотенузу трикутника CAB  і утворює з катетами  трикутника CAB  кути, що рівні  45°. Точка  L ділить гіпотенузу на відрізки, довжини яких рівні:

АL = bс/ (а+ b);

BL = aс/ (а+ b).

  Бісектриса  СL являється  діагоналлю квадрата KLMС і квадрат бісектриси знаходимо за формулою Лагранжа: 

CL² = BC∙CA - BL∙LA

CL = (ab  - [bс/ (а+ b)] ∙ [aс/ (а+ b)])^0,5.

CL = 1/(a+b)∙[ ab∙(a+b+c)∙(a+b-c) ]^0,5,  де с =  (b² + а²) ^0,5.

Згідно формули зв’язку між діагоналлю квадрата  d та стороною  n, отримаємо, що

d = n∙2^0,5,  або  n = 0,5∙2^0,5d.

Враховуючи, що 

ML = LK = KС = MС = n = 0,5∙2^0,5d = 0,5∙2^0,5∙CL =  0,5∙2^0,5/(a+b)∙[ ab∙(a+b+c)∙(a+b-c) ]^0,5,  де с =  (b² + а²) ^0,5.

Відповідь:  0,5∙2^0,5/(a+b)∙[ ab∙(a+b+c)∙(a+b-c) ]^0,5,  де с  =  (b² + а²) ^0,5.

Задача 3. Квадрат KLMС вписаний в прямокутний трикутник ABC (<С = 90°) з відомими катетами  a, b так, що дві сторони KС  i  СM лежать на катетах ВС та СА відповідно, а одна вершина  цього квадрата лежить на гіпотенузі . Знайти відношення площ  квадрата KLMС та площі  трикутника  ABC.  При яких значеннях a  і b це відношення  площ набуває найбільшого значення?

Розв’язання.

Нехай  дано прямокутний трикутник ABC (<С = 90°) з відомими катетами  a = BC, b = AC. Використаємо формулу cторони квадрата  KLMС, яка отримана при розв’язуванні задачі 2. Знайдемо площу квадрата KLMС:

S_KLMC = KL² = 0,5∙2^0,5/(a+b)∙[ ab∙(a+b+c)∙(a+b-c) ]^0,5 ∙ 0,5∙2^0,5/(a+b)∙[ ab∙(a+b+c)∙(a+b-c) ]^0,5 = a²b²/(a+b)².

S_KLMC :S_ABC = [a²b²/(a+b)²]:[ 0,5ab]= 2 ab/(a+b)² = 2:(2  +  a/b  + b/a).

Так  як для додатніх значень  a  і b  виконується  нерівність 

a/b  + b/a  ≥ 2,

то

2  +  a/b  + b/a  ≥ 4.

Таким чином, 

S_KLMC :S_ABC = 2:(2  +  a/b  + b/a) ≤ 2:4 = 1:2 = 0,5.

Площа прямокутного  трикутника АВС може бути  вдвічі більша, ніж  площа вписаного квадрата KLMС тільки для прямокутного рівнобедреного трикутника, тобто, якщо а = b.

Відповідь: S_KLMC :S_ABC = 2:(2  +  a/b  + b/a).  Якщо а = b, то S_KLMC :S_ABC = 0,5 – це найбільше значення.

Задача 4.  Квадрат називається вписаним в прямокутний трикутник, якщо усі чотири вершини лежать на сторонах прямокутного трикутника. Знайти відношення площ  двох різних вписаних квадратів в один прямокутний трикутник.  Чи можуть ці квадрати мати однакову площу?

 

 

Розв’язання.

Площа вписаного квадрата, одна вершина якого  лежить на гіпотенузі, строго більша, ніж площа вписаного квадрата, дві вершини  якого  лежить на гіпотенузі . Покажимо це.

Площа вписаного квадрата KLMC, одна вершина якого  лежить на гіпотенузі,  рівна

S_KLMC  = a²b²/(a+b)²,

де  а  та b – катети прямокутного трикутника ( це слідує із задачі 3).

Площа вписаного квадрата ABCD, дві вершини  якого  лежить на гіпотенузі ,  рівна 

S_ABCD  = a² b² c² / (c²+ ba)² ,

де  а  та b – катети,  с – гіпотенуза  прямокутного трикутника ( це слідує із задачі 1).

S_KLMC :S_ABCD = [a²b²/(a+b)² ]: [a² b² c² / (c²+ ba)² ] = [(c²+ ba):(a+b)c ]²  >1 . Отже, S_KLMC >S_ABCD.

Відповідь: S_KLMC :S_ABCD = [(c²+ ba):(a+b)c ]².  Не можуть два різні вписані квадрати мати однакову площу.

Отже, два вписані квадрати  в прямокутний трикутник не можуть бути рівними.

Квадрат, вписаний в прямокутний трикутник з гострим кутом 30°.

Задача 5.  Знайти сторону вписаного квадрата в прямокутний трикутник з гострим кутом 30° та протилежним катетом  а, якщо дві вершини квадрата лежать на гіпотенузі, а дві інші вершини лежать на катетах.

Розв’язання.

Нехай АВС – прямокутний трикутник  з стороною  а, та KLMN - вписаний квадрат  в трикутник АВС.  До речі, використовуючи гомотетію таких вписаних квадратів в прямокутний трикутник можна побудувати один.

Нехай сторона вписаного квадрата рівна z, тоді  в прямокутному трикутнику LBM:

ÐМ = 90°, ÐL = 30°, ÐB = 60°,

згідно його властивостей  

СL = 0,5z,  LB = х = a – 0,5z, LM = z, MB = 0,5(a - 0,5z).

За теоремою Піфагора складаємо квадратне рівняння відносно  z:

(a – 0,5z)² = z² + 0,25(a - 0,5z)².

Звідси отримаємо

KL= LM = MN = KM = z = 2∙3^0,5∙a:(4+3^0,5)

CL = x = 3^0,5∙a:(4+3^0,5)

CK = y =3∙a:(4+3^0,5)

Відповідь: 3∙a:(4+3^0,5) одиниць довжини.

Задача 6.  Знайти сторону вписаного квадрата в рівносторонній  трикутник  з стороною  а.

Розв’язання.

Нехай АВС – правильний трикутник  з стороною  а, та KLMN - вписаний квадрат  в трикутник АВС.  До речі, використовуючи гомотетію таких вписаних квадратів в правильний трикутник можна побудувати три.

Нехай сторона вписаного квадрата рівна z, тоді  в прямокутному трикутнику LBM:

<М = 90°, <L = 30°, <B = 60°,

згідно його властивостей  

LB = a –z, LM = z, MB = 0,5(a - z).

За теоремою Піфагора складаємо рівняння:

(a –z)² = z² + 0,25(a - z)².

Знайдемо  невідоме  z з квадратного рівняння:

z² + 6аz² + 3a² = 0

z₁  =  (- 2∙3^0,5 – 3)a(не задовільняє умові задачі)

z₂  =  (2∙3^0,5 – 3)a

Отже, сторона  квадрата:

CL = CK = KL= LM = MN = KM = z = (2∙3^0,5 – 3)a,

Гіпотенуза та менший катет прямокутного LBM:

NА = МВ = (2 - 3^0,5)a,

KА = LВ  =  (4 - 2∙3^0,5)a,

Відповідь: (2∙3^0,5 – 3)a одиниць довжини.

Завдання для самостійних досліджень.

1. В прямокутний трикутник АВС(<C =90°)  вписаний квадрат KLMN, дві якого вершини N i M лежать на гіпотенузі. Знайдіть довжини відрізків, що утворюються  на катетах, на гіпотенузі.