Задача 1(властивості трапеції
Вінницького).
У
трапеції ABCD діагоналі перпендикулярні, а діагональ AC дорівнює
середній лінії трапеції. Знайдіть кути, які утворюють діагоналі з основами.
Розв’язування. Нехай AB –
більша основа трапеції. CD –менша основа трапеції. АС- менша діагональ трапеції. Тоді перша
середня лінія трапеції FE(DE=EA, BF=FC). FE=AC за умовою.
Діагоналі СА та BD перетинають в точці Т і
перетинають середню лінію FE в
точках S, P відповідно. Проведемо другу середню лінію КМ між
основами трапеції. Зазначимо, що точка К ділить навпіл меншу основу
трапеції, а точка М ділить навпіл більшу основу трапеції. Точка О – це точка
перетину двох середніх ліній трапеції. Тоді FO – дорівнює
половині діагоналі АС. Розглянемо трикутник OKE. За
властивістю середньої лінії трикутника, отримаємо КЕ=ЕО=0,5АС.
Таким чином, отримаємо два подібних рівнобедрених
трикутника ОКЕ та OST за спільним кутом КОЕ та пропорційними
паралельними сторонами ОЕ та ОS(згідно теореми Фалеса).
Розглянемо прямокутний трикутник
РТS, кут Т – прямий за умовою, РО=ОS= SТ=0,5РS. Отже, гострий кут ТРS=30о, кут
РSТ=60о. Два прямокутні трикутники ВТА та
РТS подібні за пропорційними сторонами та спільним кутом між ними(за
теоремою Фалеса). У подібних прямокутних трикутників рівні
відповідні кути. Таким чином, кут САВ=60о, а кут DВА = 30о.
Відповідь: 30о та
60о.
Властивості
трапеції Вінницького з перпендикулярними
діагоналями та однією рівною діагоналлю середній лінії(тобто, у даної
трапеції дві рівні середні лінії, що дорівнюють меншій діагоналі):
Якщо менша діагональ трапеції дорівнює d,(тобто, довжині середньої лінії) тоді:
1) менша основа даної трапеції дорівнює половині від довжини середньої
лінії(тобто 0,5d),
2) більша основа даної трапеції дорівнює півтора від довжини середньої
лінії, тобто 1,5d,
3)висота даної трапеції дорівнює середньому геометричному довжин основ, тобто 0,5d*30,5,
4)більша діагональ даної трапеції
дорівнює d*30,5.
5)менша бічна сторона дорівнює
висоті трапеції, 0,5d*30,5,
6)більша бічна сторона дорівнює трапеції,
0,5d*70,5,
7)площа даної трапеції рівна 0,5d2*30,5.
8)Периметр прямокутника,
побудованого на серединах сторін даної трапеції дорівнює сумі довжин двох діагоналей
даної трапеції d(1+ 30,5).
9)Площа прямокутника, побудованого
на серединах сторін даної трапеції дорівнює половині площі даної трапеції 0,25d2*30,5.
10)кожна діагональ даної трапеції в
точці перетину ділиться на частини, як DC:AB, рахуючи від більшого кута(меншої основи
трапеції).
11)гострий найменший кут даної
трапеції при більшій основі, з вершини якого виходить більша діагональ,
дорівнює arctg(0,5*30,5) радіан.
12)найбільший кут даної трапеції дорівнює p- arctg(0,5*30,5) радіан.
13)середні два кути трапеції прямі,
90о.
14)навколо даної трапеції не можна описати
коло.
15) в дану трапеції не можна
вписати коло.
16)діагоналі ділять середню лінію трапеції на такі три відрізки,
що мають довжину 0,25d , 0,5d,
0,25d.
17) Середні лінії даної трапеції в
точці перетину діляться навпіл.
Діагоналі рівнобічної трапеції
взаємно перпендикулярні, і поділяють середню лінію трапеції на три рівні
відрізки. Знайдіть висоту трапеції, якщо більша основа дорівнює 12 см.
Відповідь: 9 см.
Гіпотеза Вінницького. Довжини двох середніх ліній, довжини двох
діагоналей, місце розташування точки перетину двох середніх ліній і точки
перетину двох діагоналей випуклого чотирикутника, поділ точкою перетину на дві
частини діагоналей, поділ точкою перетину середніх ліній на дві частини, кут
між двома середніми лініями та кут між двома діагоналями випуклого чотирикутника
однозначно визначають усі властивості даного чотирикутника.
2)При яких значеннях кута ВАС можна гарантувати, що довжина однієї діагоналі буде дорівнювати двом довжинам іншої діагоналі?
Означення. Трапеція називається прямокутною
трапецією Вінницького, якщо вона прямокутна і довжина висоти трапеції
дорівнює середньому геометричному довжин
її основ.
Задача 2 Вінницького. Прямокутна трапеція Вінницького з довжинами основ а
та b(a<b,
a||b), має довжину висоти,
що дорівнює середньому геометричному основ даної трапеції, тобто (ab)0,5.
Доведіть:
1)прямий кут
DOA між діагоналями даної трапеції;
2) довжина
більшої бічної сторони BC=u= (а2-ab+b2)0,5;
3)довжина
АО=m=a(b/(a+b))0,5;
4) довжина
CО=n=b(b/(a+b))0,5;
5) довжина
OD=t=b(a/(a+b))0,5;
6) довжина
BО=p=a(a/(a+b))0,5;
7) кут DCB
= arctg((ab)0,5/(a+b)) радіан;
8) кут АBС
= p-arctg((ab)0,5/(a+b))
радіан;
9) діагоналі
ділять середню лінію на довжини r=w=0,5a та z=0,5(b-a);
10) кут DCА
= arctg(a/b)0,5 радіан;
11) кут ВDC
=0,5p- arctg(a/b)0,5
радіан;
12)
трикутник ВDC- гострокутний;
13)точка перетину діагоналей ділить лінію, що паралельна основам, на два рівні відрізки FO=OG= ab/(a+b).
Критерій Вінницького. Якщо прямокутна трапеція має
перпендикулярні діагоналі, то довжина висоти трапеції дорівнює середньому
геометричному довжин її основ, і
навпаки, якщо довжина висоти прямокутної трапеції дорівнює середньому
геометричному її основ, то кут між діагоналями даної трапеції прямий.
Проблемні запитання до умови задачі 3.
1)При яких значеннях кута ВАС можна гарантувати, що довжина однієї діагоналі буде дорівнювати довжині середньої лінії?
Розв’язування:
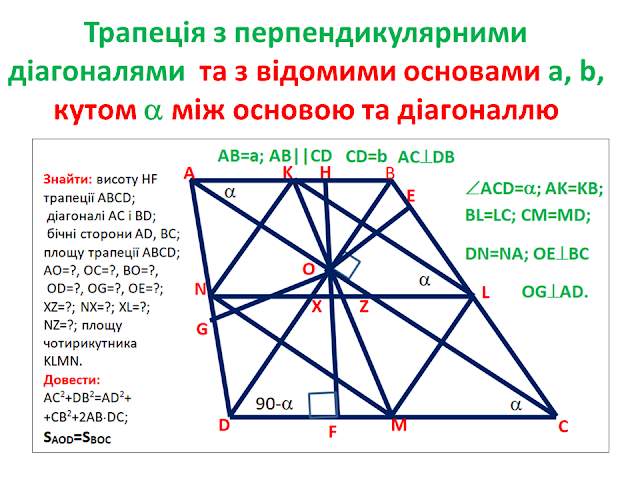
ABCD- трапеція з перпендикулярними діагоналями, що перетинаються в точці О.
АВ=а, DC=b, ÐACD=a, ÐAOB- прямий, AK=KB, BL=LC,
CM=MD, DG=GA, KM – середня лінія трапеції,
NL – середня лінія трапеції.
HF= 0,5(a+b)sin2a - висота трапеції ABCD.
S=0,25(a+b)2sin2a - площа трапеції
ABCD.
d1=DB=(a+b)sina - діагональ трапеції ABCD.
d2=АС=(a+b)cosa - діагональ трапеції ABCD.
KM=NL=0,5(a+b)- середні лінії трапеції.
NX=LZ=0,5a; XZ=0,5(b-a);
ВС= (b2cos2a + a2sin2a)0,5 - бічна сторона трапеції ABCD.
AD= (а2cos2a + b2sin2a)0,5 - бічна сторона трапеції ABCD.
OE=(0,5absin2a)/ (b2cos2a + a2sin2a)0,5
OG=(0,5absin2a)/ (а2cos2a + b2sin2a)0,5
Два подібні прямокутні
трикутники AOB та COD,
що містять основи трапеції з коефіцієнтом подібності k=b/a.
Два подібні прямокутні
трикутники AOB та LNK,
що відповідно містять основу та середню лінію трапеції
з коефіцієнтом
подібності k=0,5(1+b/a).
Два подібні прямокутні
трикутники AOB та ZOX,
з коефіцієнтом
подібності k=2a/(b-a).
Два подібні прямокутні
трикутники COD та ZOX,
з коефіцієнтом
подібності k=2b/(b-a).
Два рівновеликі (проте
не подібні) прямокутні трикутники АOD та ВOС,
з рівними площами S=0,25absin2a.
S=0,125(a+b)2sin2a- це площа прямокутника KLMN,
що побудований
на серединах сторін трапеції ABCD.
Проблемні запитання до умови задачі 3.
1)При яких значеннях кута ВАС можна гарантувати, що довжина однієї діагоналі буде дорівнювати довжині середньої лінії?
3)При яких значеннях кута ВАС можна гарантувати, що довжини двох діагоналей буде дорівнювати одна одній?
Теорема.
У прямокутну трапецію Вінницького (з
перпендикулярними діагоналями) не можна вписати коло.
Задача 4(Вінницького) для самостійного опрацювання.
Якщо у прямокутній трапеції Вінницького ABCD (AB||CD, кут А – прямий, кут D – прямий, кут В – тупий, кут С – гострий, діагоналі АС та DB перетинаються під прямим кутом) відома довжина більшої основи CD=a, відомий кут BDC, між діагоналлю, що виходить з тупого кута, та довільною основою дорівнює дві третини прямого кута, тобто 60о, тоді обґрунтуйте такі твердження:
Якщо у прямокутній трапеції Вінницького ABCD (AB||CD, кут А – прямий, кут D – прямий, кут В – тупий, кут С – гострий, діагоналі АС та DB перетинаються під прямим кутом) відома довжина більшої основи CD=a, відомий кут BDC, між діагоналлю, що виходить з тупого кута, та довільною основою дорівнює дві третини прямого кута, тобто 60о, тоді обґрунтуйте такі твердження:
А) кут DСА = 30о, кут DСА = 30о , кут JZY= 30о;
Б) довжини діагоналей трапеції ABCD: АС =2а/(3)0,5
та DB = 2а/3, при цьому діагоналі АС та DB перетинаються під прямим кутом;
В) довжини сторін трапеції ABCD: більша основа: DC=a; менша бічна: DA= а/(3)0,5;
менша
основа: AB= a/3; більша бічна:
BC= а(7)0,5/3;
Г) подібні прямокутні
трикутники ( за рівними
кутами: 30о; 90о; 60о ): DOC,
XOZ, AOB,
NKL, NML, ABD, MLC, KLM, NKM, BHP, DBH.
Д) правильні трикутники: 1) рівносторонній
трикутник DOM з
сторонами DO=OM=DM=0,5a; 2) рівні
рівносторонні трикутники з довжиною сторони, що дорівнює а/3:
NKY, XBZ, DZH, YML; 3)
два рівні рівносторонні трикутники КOВ та ХОУ з сторонами КO=OВ=КВ=a/6;
Є) AK=KB,
BL=LC, CM=MD, DN=NA, KLNM – прямокутник з
довжинами сторін, NK=LM=a/3; KL=NM=a/(3)0,5.
Ж)ABZX
– ромб з довжинами
усіх сторін (AB=AX=XZ=BZ=BX), що дорівнюють а/3.
З) DH=HP=HC=NY=YL=AB=a/3.
З) DH=HP=HC=NY=YL=AB=a/3.
Проблемне запитання: Чи може трапеція Вінницького бути рівнобічною? Теорема.
а) висота дорівнює 0,5d(2)0,5, d – діагональ рівнобічної трапеції;
б)бічну сторону рівнобічної трапеції з центру описаного кола видно під прямим кутом;
в)кут між діагоналлю та основою рівнобічної трапеції дорівнює половині прямого кута(45 градусів);
г) чотирикутник зі усіма рівними сторонами 0,5d, що побудований на серединах усіх сторін рівнобічної трапеції являється квадратом, при цьому діагоналі цього квадрата є середніми лініями рівнобічної трапеції;
д) діагональ d не дорівнює середній лінії трапеції 0,5d(2)0,5 (тобто середня лінія менша, ніж діагональ, тому жодна рівнобічна трапецією не може бути трапецією Вінницького).


б)бічну сторону рівнобічної трапеції з центру описаного кола видно під прямим кутом;
в)кут між діагоналлю та основою рівнобічної трапеції дорівнює половині прямого кута(45 градусів);
г) чотирикутник зі усіма рівними сторонами 0,5d, що побудований на серединах усіх сторін рівнобічної трапеції являється квадратом, при цьому діагоналі цього квадрата є середніми лініями рівнобічної трапеції;
д) діагональ d не дорівнює середній лінії трапеції 0,5d(2)0,5 (тобто середня лінія менша, ніж діагональ, тому жодна рівнобічна трапецією не може бути трапецією Вінницького).



















Коментарі