Правильний шестикутник

Означення. Правильний многокутника — це многокутника, у якого всі сторони та кути однакові.

Многокутником називається частина площі, яка обмежена замкненою ламаною лінією, що не перетинає сама себе.

Многокутники відрізняються між собою кількістю сторін та кутів.

Правильний шестикутник

Формули правильного шестикутника:

1. Формула сторони правильного шестикутника через радіус вписаного кола:

a =	2√3	r
	3

2. Формула сторони правильного шестикутника через радіус вписаного кола:

a = R

3. Формула радіусу кола вписаного в правильний шестикутник через довжину сторони:

r =	a√3
	2

4. Формула радіуса кола описаного навколо правильного шестикутника через довжину сторони:

R = a

5. Формула площі правильного шестикутника через довжину сторони:

S =	a2 3√3
	2

6. Формула площі правильного шестикутника через радіус вписаного кола:

S = r² 2√3

7. Формула площі правильного шестикутника через радіус описаного кола:

S =	R2 3√3
	2

8. Кут між сторонами правильного шестикутника:

α = 120°

Основні властивості правильного многокутника

1. Всі сторони рівні:
a₁ = a₂ = a₃ = ... = a_n-1 = a_n

2. Всі кути рівні:
α₁ = α₂ = α₃ = ... = α_n-1 = α_n

3. Центр вписаного кола O_в співпадає з центром описаного кола O_о, і вони утворюють центр многокутника O

4. Сума всіх кутів n-кутника дорівнює:

180° · (n - 2)

5. Сума всіх зовнішніх кутів n-кутника кутника 360°:

β₁ + β₂ + β₃ + ... + β_n-1 + β_n = 360°

6. Кількість діагоналей (D_n) n-кутника дорівнює половині добутку кількості вершин на кількість діагоналей, що виходять з кожної вершини:

Dn =	n · (n - 3)
	2

7. В будь який многокутник можна вписати коло та описати круг при цьому площа кільця, утвореного цими колами, залежить тільки від довжини сторони многокутника:

S =	π	a2
	4

8. Всі бісектриси кутів між сторонами рівні і проходять через центр правильного многокутника O

Вписані багатокутники в правильний шестикутник





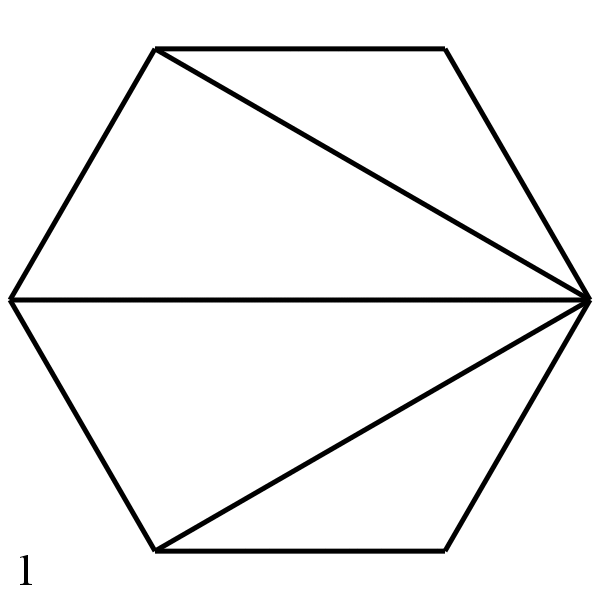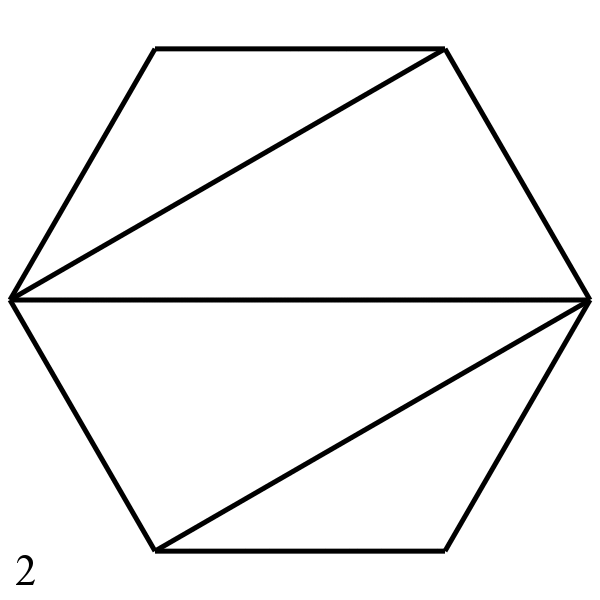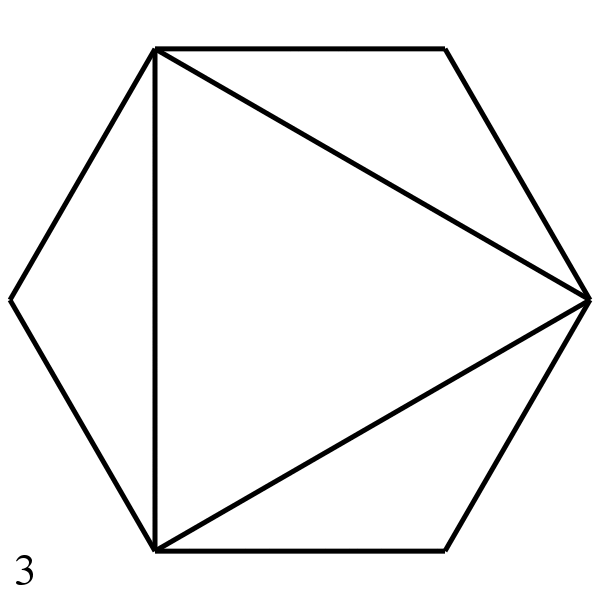
Зовнішні кути шестикутника, їх сума дорівнює  360 градусів


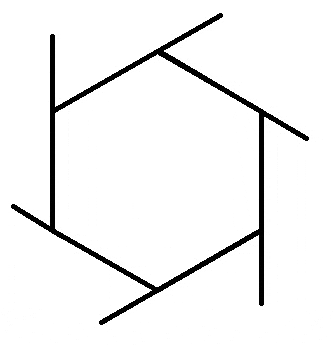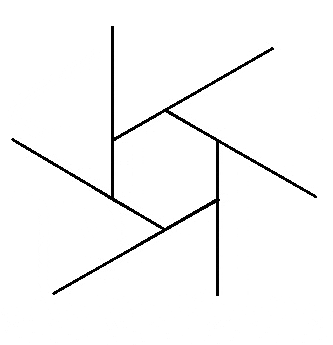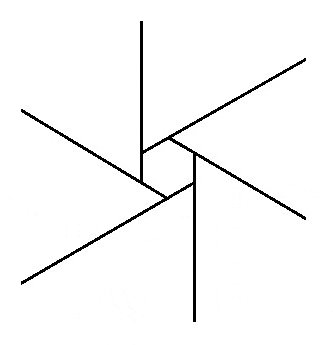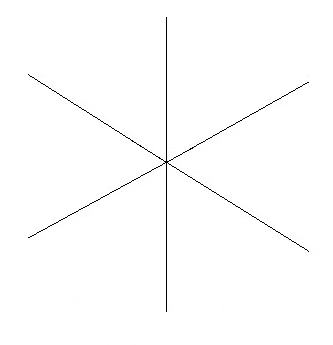
Графіки зміни координат точок  фігури

Рис.3

Правильний трикутник

Формули правильного трикутника:

1. Формула сторони правильного трикутника через радіус вписаного кола:

a = 2r √3

2. Формула сторони правильного трикутника через радіус описаного кола:

a = R√3

3. Формула радіусу кола вписаного в правильний трикутник через довжину сторони:

r =	a√3
	6

4. Формула радіуса кола описаного навколо правильного трикутника через довжину сторони:

R =	a√3
	3

5. Формула площі правильного трикутника через довжину сторони:

S =	a2√3
	4

6. Формула площі правильного трикутника через радіус вписаного кола:

S = r² 3√3

7. Формула площі правильного трикутника через радіус описаного кола:

S =	R2 3√3
	4

8. Кут між сторонами правильного трикутника:

α = 60°

Правильний чотирикутник

Правильний чотирикутник - квадрат.

Формули правильного чотирикутника:

1. Формула сторони правильного чотирикутника через радіус вписаного кола:

a = 2r

2. Формула сторони правильного чотирикутника через радіус описаного кола:

a = R√2

3. Формула радіусу кола вписаного в правильний чотирикутник через довжину сторони:

r =	a
	2

4. Формула радіуса кола описаного навколо правильного чотирикутника через довжину сторони:

R =	a√2
	2

5. Формула площі правильного чотирикутника через довжину сторони:

S = a²

6. Формула площі правильного чотирикутника через радіус вписаного кола:

S = 4 r²

7. Формула площі правильного чотирикутника через радіус описаного кола:

S =  2 R²

8. Кут між сторонами правильного чотирикутника:

α = 90°