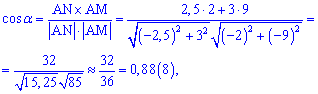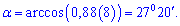Задача про трикутник на площині
Досить часто на практичних заняттях доводиться обчислювати задачу про трикутник на площині. Суть її полягає в тому, що відомо три точки, які не лежать на одній прямій - утворюють трикутник. Потрібно скласти рівняння сторін, висот, медіан і бісектрис, також часто і кути між сторонами трикутниа. Завдання не складні в плані обчислень, проте добре потрібно знати властивості векторного та скалярного добутку. Нижче наведена схема обчислення трикутника на площині.
Також вкінці для Вас бонус - математичний калькуятор під відовс, який обчилює задачу про трикутник на площині на автоматі. Достатньо лише ввести три точки і за секунду любуватися результатом. Скачати калькулятор можуть всі, його розповсюдження є безкоштовним.
Також вкінці для Вас бонус - математичний калькуятор під відовс, який обчилює задачу про трикутник на площині на автоматі. Достатньо лише ввести три точки і за секунду любуватися результатом. Скачати калькулятор можуть всі, його розповсюдження є безкоштовним.
Приклад 1. На площині задано трикутник 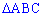 з вершинами
з вершинами
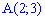 ,
, 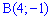 ,
, 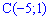 .
.
 з вершинами
з вершинами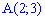 ,
, 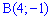 ,
, 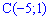 .
.
Потрібно знайти:
1) довжину сторони 
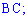



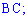


2) скласти загальне рівняння медіани, висоти та бісектриси кута 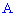 ;
;
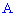 ;
;
3) знайти відстань від вершини  до медіани;
до медіани;
 до медіани;
до медіани;
4) знайти кут між медіаною і висотою (у градусах).
Розв'язок.
1) Довжина сторони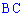
1) Довжина сторони
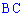
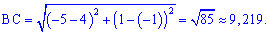
2) Загальне рівняння медіани, висоти та бісектриси кута
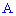
Побудуємо рівняння медіани, яка ділить протилежну сторону пополам в точці
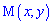 . Знайдемо її
. Знайдемо її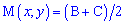
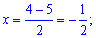
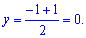
Побудуємо загальне рівняння прямої, що проходить через точки
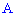 та
та 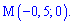
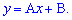
При підстановці точок отримаємо систему двох рівнянь
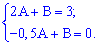
Віднімемо від першого рівняння друге
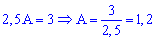
Отримане значення підставляємо в перше рівняння
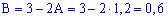 .
.
Рівняння 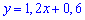
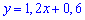
Остаточне рівняння медіани матиме вигляд
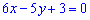 .
.
Складемо загальне рівняння висоти 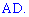
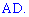
Для цього знайдемо кутовий коефіцієнт сторони 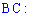
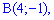
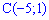
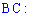
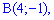
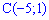
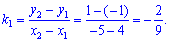
Кутовий коефіцієнт висоти, проведеної з вершини 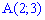 рівний
рівний
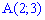 рівний
рівний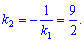
Рівняння висоти, що проходить через точку 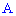 має вигляд
має вигляд
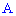 має вигляд
має вигляд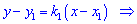
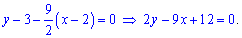
Знайдемо рівняння бісектриси 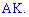 За означенням бісектриса ділить кут пополам, тому
За означенням бісектриса ділить кут пополам, тому 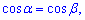 де
де
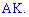 За означенням бісектриса ділить кут пополам, тому
За означенням бісектриса ділить кут пополам, тому 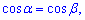 де
де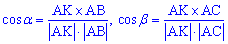
З рівності кутів випливає залежність для визначення рівняння бісектриси
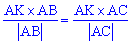
Знайдемо складові рівняння
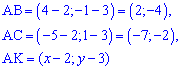
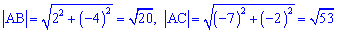
Підставимо знайдені значення у рівняння
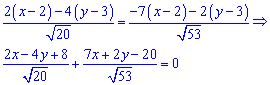
або після спрощень

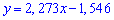
3) відстань від вершини B до медіани Знайдемо відстань від вершини 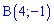 до медіани
до медіани 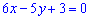 за форомулою
за форомулою
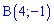 до медіани
до медіани 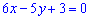 за форомулою
за форомулою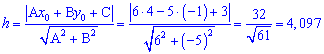
4) Кут між медіаною і висотою
Маємо дві точки медіани 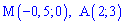 і рівняння висоти
і рівняння висоти 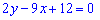 . Виберемо другу точку
. Виберемо другу точку 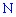 з рівняння висоти:
з рівняння висоти: 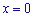 , знаходимо
, знаходимо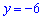 . Обчислимо
. Обчислимо
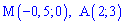 і рівняння висоти
і рівняння висоти 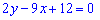 . Виберемо другу точку
. Виберемо другу точку 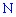 з рівняння висоти:
з рівняння висоти: 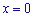 , знаходимо
, знаходимо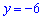 . Обчислимо
. Обчислимо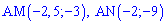
Знайдемо косинус кута між векторами